题目内容
已知点 直线AM,BM相交于点M,且
直线AM,BM相交于点M,且 .
.
(1)求点M的轨迹 的方程;
的方程;
(2)过定点(0,1)作直线PQ与曲线C交于P,Q两点,且 ,求直线PQ的方程.
,求直线PQ的方程.
(1)
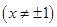 ; (2)
; (2)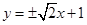 .
.
解析试题分析:(1)先设出点 的坐标,根据两点间的斜率公式求出
的坐标,根据两点间的斜率公式求出 和
和 ,代入已知条件
,代入已知条件 中,化简整理得
中,化简整理得
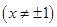 ,限制条件一定要有;(2)分直线
,限制条件一定要有;(2)分直线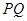 的斜率存在与不存在两种情况进行讨论,当斜率存在时,设出直线方程及与曲线的交点坐标,联立方程由方程的根与系数的关系求得
的斜率存在与不存在两种情况进行讨论,当斜率存在时,设出直线方程及与曲线的交点坐标,联立方程由方程的根与系数的关系求得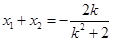 ,
, ,代入
,代入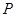 、
、 两点间的距离公式并化简,结合已知条件
两点间的距离公式并化简,结合已知条件 求得
求得 的值,代入所设的直线方程即可.
的值,代入所设的直线方程即可.
试题解析:(1)解:设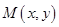 , ..1分
, ..1分
则 ,
, , .3分
, .3分
∴ , .4分
, .4分
∴
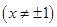 . .6分 (条件1分)
. .6分 (条件1分)
(2)当直线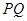 的斜率不存在时,即
的斜率不存在时,即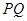 是椭圆的长轴,其长为
是椭圆的长轴,其长为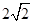 ,显然不合,
,显然不合,
所以直线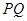 的斜率存在, 7分
的斜率存在, 7分
设直线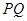 的方程是
的方程是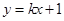 ,
,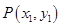 ,
, ,
,
则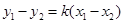 , .8分
, .8分
联立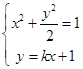 ,消去
,消去 得
得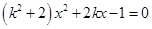 , 9分
, 9分
∵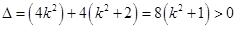 ,∴
,∴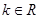 , ..10分
, ..10分
∴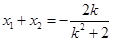 ,
, , .11分
, .11分
∴
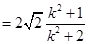 , ..12分
, ..12分
∴
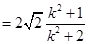 ,∴
,∴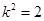 ,即
,即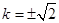 , .13分
, .13分
所以直线PQ的方程是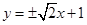 . ..14分
. ..14分
考点:1.直线的斜率;2.方程的根与系数的关系;3.分类讨论思想;4.两点间的距离公式;5.直线方程;6.轨迹方程

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 是定义域为
是定义域为 的单调减函数,且是奇函数,当
的单调减函数,且是奇函数,当 时,
时,
 的不等式
的不等式
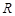 的函数
的函数 是奇函数.
是奇函数. 值;
值; 的函数
的函数 有零点,求实数
有零点,求实数 的取值范围.
的取值范围. 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于 万元,同时不超过投资收益的
万元,同时不超过投资收益的 .
. ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型 ; ②
; ②

 在
在 上的最大值与最小值之和为
上的最大值与最小值之和为 ,记
,记 .
. 的值;
的值; ;
; 的值.
的值. 且
且 .
. 的值;
的值; 在
在 上的单调性,并给予证明.
上的单调性,并给予证明. ,满足
,满足 ,且方程
,且方程 有两个相等的实根.
有两个相等的实根. 的解析式;
的解析式;
 时,求函数
时,求函数 的表达式.
的表达式. 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, .
.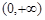 上的单调性.
上的单调性. 上的函数
上的函数 同时满足:①
同时满足:① ;②
;② ;③若
;③若 ,且
,且 ,则
,则 成立.则称函数
成立.则称函数 在区间
在区间