题目内容
已知二次函数 ,满足
,满足 ,且方程
,且方程 有两个相等的实根.
有两个相等的实根.
(1)求函数 的解析式;
的解析式;
(2)当
 时,求函数
时,求函数 的最小值
的最小值 的表达式.
的表达式.
(1) ;(2)
;(2)
解析试题分析:(1)应用结论:函数 满足
满足 ,则直线
,则直线 是函数
是函数 图象的对称轴,一般地函数
图象的对称轴,一般地函数 满足
满足 ,则直线
,则直线 是函数
是函数 图象的对称轴.(2)二次函数
图象的对称轴.(2)二次函数 在区间
在区间 上单调递减,在区间
上单调递减,在区间 上单调递增,我们在求二次函数在区间
上单调递增,我们在求二次函数在区间 上的最值时,要特别注意
上的最值时,要特别注意 与
与 的关系,也即要讨论
的关系,也即要讨论 在区间
在区间 上单调性,则单调性得出最值.
上单调性,则单调性得出最值.
试题解析:解:(1)由 ,得:对称轴
,得:对称轴 ,
,
由方程 有两个相等的实根可得:
有两个相等的实根可得: ,
,
解得 .
.
∴ . 5分
. 5分
(2) .
.
①当 ,即
,即 时,
时, ; 6分
; 6分
②当 ,即
,即 时,
时, ; 8分[
; 8分[
③当 时,
时, ; 10分
; 10分
综上: . 12分
. 12分
考点:1、函数图象的对称性;2、二次函数在给定区间的最值.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 ,
, 是
是 上的奇函数.
上的奇函数. 的值;
的值; 在
在 .
.
 是奇函数,并且函数
是奇函数,并且函数 的图像经过点(1,3),(1)求实数
的图像经过点(1,3),(1)求实数 的值;(2)求函数
的值;(2)求函数 直线AM,BM相交于点M,且
直线AM,BM相交于点M,且 .
. 的方程;
的方程; ,求直线PQ的方程.
,求直线PQ的方程. 为奇函数,且当
为奇函数,且当 时,
时, .当
.当 时,
时, ,最小值为
,最小值为 ,求
,求 的值.
的值. .(I)求函数
.(I)求函数 的单调递增区间;
的单调递增区间;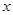 的方程
的方程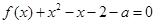 在区间
在区间 内恰有两个不同的实根,求实数
内恰有两个不同的实根,求实数 的取值范围.
的取值范围. ,是否存在实数a、b、c,使
,是否存在实数a、b、c,使 同时满足下列三个条件:(1)定义域为R的奇函数;(2)在
同时满足下列三个条件:(1)定义域为R的奇函数;(2)在 上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由.
上是增函数;(3)最大值是1.若存在,求出a、b、c;若不存在,说明理由. ,
, ,
, 的定义域为
的定义域为
 的值;
的值; 在区间
在区间 的取值范围。
的取值范围。 ,其中e为自然对数的底数,且当x>0时
,其中e为自然对数的底数,且当x>0时 恒成立.
恒成立. 的单调区间;
的单调区间; .
.