题目内容
15．函数f（x）=$\frac{1}{3}$x3-$\frac{1}{2}$（m+1）x2+2（m-1）x在（0，4）上无极值，则m=3．分析 函数f（x）在（0，4）上无极值即导函数f'（x）在（0，4）上无根，f'（x）=x2-（m+1）x+2（m-1）在（0，4）上恒有f'（x）≥0．
解答 解：函数f（x）在（0，4）上无极值即导函数f'（x）在（0，4）上无根．
f'（x）=x2-（m+1）x+2（m-1）在（0，4）上恒有f'（x）≥0 ①；
当m-1＞2时，①式解为x≤2 或 x≥m-1；显然x∈（0，4）时，①式不成立；
当m-1＜2时，①式解为x≤m-1或x＞2；显然x∈（0，4）时，①式不成立；
当m-1=2时，①式解为x=2，m=3．
故答案为：3．
点评 本题主要考查了导函数零点与极值关系，以及二次函数在特定区间求值，属中等题．
练习册系列答案
相关题目
6．已知偶函数f（x）在区间[0，+∞）上是增函数，则f（-1）与f（2）的大小关系是（ ）
| A． | f（-1）≥f（2） | B． | f（-1）≤f（2） | C． | f（-1）＞f（2） | D． | f（-1）＜f（2） |
20．阅读下面的程序框图，运行相应的程序，输出的结果为（ ）
| A． | $\frac{21}{13}$ | B． | $\frac{13}{8}$ | C． | $\frac{34}{21}$ | D． | $\frac{8}{5}$ |
7．
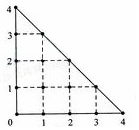某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横的交叉点以及三角形的顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获量Y（单位：kg）与它的“相近”作物株数X之间的关系如表所示：
这里，两株作物“相近”是指它们之间的直线距离不超过1米．
（1）从三角形地块的内部和边界上分别随机选取一株作物，求它们恰好“相近”的概率；
（2）从所种作物中随机选取一株，求它的年收获量Y的分布列．
某人在如图所示的直角边长为4米的三角形地块的每个格点（指纵、横的交叉点以及三角形的顶点）处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获量Y（单位：kg）与它的“相近”作物株数X之间的关系如表所示：| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
（1）从三角形地块的内部和边界上分别随机选取一株作物，求它们恰好“相近”的概率；
（2）从所种作物中随机选取一株，求它的年收获量Y的分布列．