题目内容
设是O是△ABC内一点,且
+2
+3
=
,则△AOC的面积与△BOC的面积之比值是( )
| OA |
| OB |
| OC |
| 0 |
分析:延长OB至B',使OB'=2OB;延长OC至C',使OC'=3OC,可得O是△AB′C′的重心,利用三角形重心的性质,即可得到结论.
解答: 解:延长OB至B',使OB'=2OB;延长OC至C',使OC'=3OC,则
解:延长OB至B',使OB'=2OB;延长OC至C',使OC'=3OC,则
+
+
=
∴O是△AB′C′的重心
∴S△AOC′=S△B′OC′,
∵S△AOC=
S△AOC′,S△BOC=
S△B′′OC′,
∴S△AOC:S△BOC=2:1,
故选C.
 解:延长OB至B',使OB'=2OB;延长OC至C',使OC'=3OC,则
解:延长OB至B',使OB'=2OB;延长OC至C',使OC'=3OC,则| OA′ |
| OB′ |
| OC′ |
| 0 |
∴O是△AB′C′的重心
∴S△AOC′=S△B′OC′,
∵S△AOC=
| 1 |
| 3 |
| 1 |
| 6 |
∴S△AOC:S△BOC=2:1,
故选C.
点评:本题主要考查三角形面积的计算,考查向量的加法法则,体现了向量在解决有关平面图形问题题中的优越性.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知O为平面内一定点,设条件p:动点M满足
=
+λ(
+
),λ∈R;条件q:点M的轨迹通过△ABC的重心.则条件p是条件q的( )
| OM |
| OA |
| AB |
| AC |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
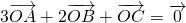 .P是△ABC内任一点,S△ABC表示△ABC的面积,记
.P是△ABC内任一点,S△ABC表示△ABC的面积,记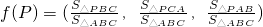 ,若
,若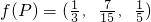 ,则
,则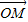 =
=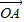 +λ(
+λ(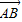 +
+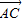 ),λ∈R;条件q:点M的轨迹通过△ABC的重心.则条件p是条件q的( )
),λ∈R;条件q:点M的轨迹通过△ABC的重心.则条件p是条件q的( )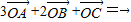 .P是△ABC内任一点,S△ABC表示△ABC的面积,记
.P是△ABC内任一点,S△ABC表示△ABC的面积,记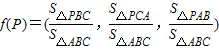 ,若
,若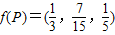 ,则( )
,则( )