题目内容
设向量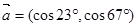 ,
,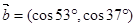 ,
,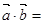 ( )
( )
A.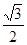 | B.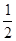 | C.-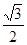 | D.-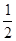 |
A
解析试题分析:因为向量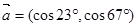 ,
,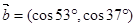 ,
,
所以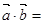

 .
.
考点:本小题主要考查平面向量的数量积和两角和与查的正弦公式以及诱导公式的应用,考查学生的运算求解能力.
点评:两角和与差的正弦、余弦公式应用十分广泛,要灵活应用.

练习册系列答案
相关题目
设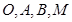 为平面上四点,
为平面上四点,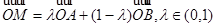 ,则
,则
A.点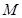 在线段 在线段 上 上 | B.点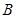 在线段 在线段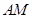 上 上 |
C.点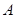 在线段 在线段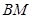 上 上 | D.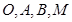 四点共线 四点共线 |
已知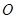 为平面上的定点,
为平面上的定点, 、
、 、
、 是平面上不共线的三点,若
是平面上不共线的三点,若
 ,则DABC是( )
,则DABC是( )
| A.以AB为底边的等腰三角形 | B.以BC为底边的等腰三角形 |
| C.以AB为斜边的直角三角形 | D.以BC为斜边的直角三角形 |
已知平面上三点A,B,C满足 ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.等腰三角形 | B.等边三角形 |
| C.直角三角形 | D.等腰直角三角形 |
已知 三点的坐标分别是
三点的坐标分别是 ,
, ,
, ,
, ,若
,若 ,则
,则 的值为( )
的值为( )
A. | B. | C.2 | D. |
在△ABC中,三边长AB=7,BC=5,AC=6,则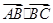 的值为( )
的值为( )
A.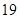 | B.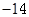 | C.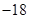 | D.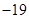 |
已知 和点M,对空间内的任意一点
和点M,对空间内的任意一点 满足,
满足, ,若
,若
存在实数m使得 ,则m=( )
,则m=( )
| A.2 | B.3 | C.4 | D.5 |
在 中,已知
中,已知 ,
, ,
, ,P为线段AB上的一点,且
,P为线段AB上的一点,且 .
. ,则
,则 的最小值为( )
的最小值为( )
A. | B. | C. | D. |
已知 为
为 的三个内角
的三个内角 的对边,向量
的对边,向量 ,
, .若
.若 ,且
,且 ,则角
,则角 ( )
( )
A. | B. | C. | D. |