题目内容
已知 三点的坐标分别是
三点的坐标分别是 ,
, ,
, ,
, ,若
,若 ,则
,则 的值为( )
的值为( )
A. | B. | C.2 | D. |
B
解析试题分析:由题意知 ,
,
所以
所以 ,
,
两边平方得
所以
考点:本小题主要考查向量数量积的坐标运算和三角函数的化简求值,考查学生的运算求解能力.
点评:三角函数的化简和求值是高考考查的重点内容,经常和向量的数量积结合考查,要适当选择三角函数的公式并灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量 ,且
,且 ,则
,则 的取值范围是( )
的取值范围是( )
A.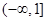 | B. | C. | D. |
在平面内,已知 ,
, ,
, ,设
,设 ,(
,( ),则
),则 等于
等于
A. | B. | C. | D. |
非零向量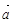 ,
,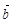 的夹角为
的夹角为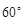 ,且
,且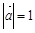 ,则
,则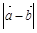 的最小值为
的最小值为
A.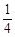 | B.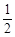 | C.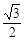 | D.1 |
已知向量 ,
, ,
, ,则
,则 = ( )
= ( )
A. | B. | C.5 | D.25 |
设向量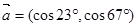 ,
,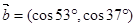 ,
,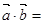 ( )
( )
A.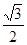 | B.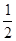 | C.-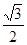 | D.-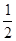 |
已知向量 夹角的取值范围是( )
夹角的取值范围是( )
A. | B. | C. | D. |
若向量 满足
满足 ,
, 与
与 的夹角为
的夹角为 ,则
,则
A. | B. | C.4 | D.12 |
已知 中,
中, 且
且 ,则
,则 的形状为:
的形状为:
| A.锐角三角形 | B.钝角三角形 | C.等腰直角三角形 | D.等边三角形 |