题目内容
4．已知sinx=$\frac{3}{5}，且\frac{π}{2}$＜x＜π，则tanx=-$\frac{3}{4}$．分析 利用同角三角函数的基本关系，以及三角函数在各个象限中的符号，求得tanx的值．
解答 解：∵sinx=$\frac{3}{5}，且\frac{π}{2}$＜x＜π，∴cosx=-$\sqrt{{1-sin}^{2}x}$=-$\frac{4}{5}$，
则tanx=$\frac{sinx}{cosx}$=-$\frac{3}{4}$，
故答案为：-$\frac{3}{4}$．
点评 本题主要考查同角三角函数的基本关系，以及三角函数在各个象限中的符号，属于基础题．
练习册系列答案
相关题目
设椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的长轴长为6，离心率$e=\frac{{\sqrt{6}}}{3}$，O为坐标原点．
19．若MP和OM分别是角$\frac{7π}{6}$的正选线和余弦线，则（ ）
| A． | MP＜OM＜0 | B． | OM＞0＞MP | C． | OM＜MP＜0 | D． | MP＞0＞OM |
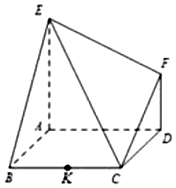如图，已知多面体EABCDF的底面ABCD是边长为2的正方形，EA⊥底面ABCD，FD∥EA，且$FD=\frac{1}{2}EA=1$．