题目内容
(本小题满分12分)在数列 中,已知
中,已知
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设数列 满足
满足 ,求
,求 的前n项和
的前n项和 .
.
(1) ,
, ;(2)
;(2) .
.
【解析】
试题分析:(1) ∴数列{
∴数列{ }是首项为
}是首项为 ,公比为
,公比为 的等比数列, 即可求出数列
的等比数列, 即可求出数列 的通项公式,将数列
的通项公式,将数列 的通项公式代入
的通项公式代入 ,即可求出结果;(2)由(1)知,
,即可求出结果;(2)由(1)知,
 ,然后再利用错位相减即可求出结果.
,然后再利用错位相减即可求出结果.
试题解析:(1)
∴数列{ }是首项为
}是首项为 ,公比为
,公比为 的等比数列, 2分
的等比数列, 2分
∴ . 4分
. 4分
∵ , ∴
, ∴ . 6分
. 6分
(2)由(1)知, ,
, (n
(n )
)
∴ .
.
∴ , ① 7分
, ① 7分
于是 ② 8分
② 8分
两式①-②相减得 9分
9分
= . 11分
. 11分
∴  . 12分.
. 12分.
考点:1.等比数列的概念;2.错位相减法求和.

练习册系列答案
相关题目
 中,侧棱垂直于底面,
中,侧棱垂直于底面, ,
, ,
, ,
, ,点
,点 在
在 上.
上.
 是
是 中点,求证:
中点,求证: 平面
平面 ;
; 时,求二面角
时,求二面角 的余弦值.
的余弦值. ,则目标函数z=2y﹣x的最大值是( )
,则目标函数z=2y﹣x的最大值是( ) 的前n项和
的前n项和 满足
满足 ,则
,则 _________.
_________. ,则
,则 ( )
( ) 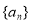 中,
中,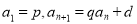 (
( N*,
N*,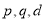 是常数),则
是常数),则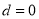 是数列
是数列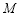 由满足:对任意
由满足:对任意 时,都有
时,都有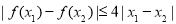 的函数
的函数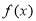 组成.对于两个函数
组成.对于两个函数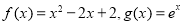 ,以下关系成立的是
,以下关系成立的是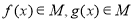 B.
B.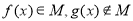
 D.
D.