题目内容
3.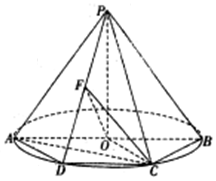 如图,AB是圆O的直径,点C,D是圆O上异于A,B的点,CD∥AB,F为PD中点,PO⊥垂直于圆O所在的平面,∠ABC=60°.
如图,AB是圆O的直径,点C,D是圆O上异于A,B的点,CD∥AB,F为PD中点,PO⊥垂直于圆O所在的平面,∠ABC=60°.(Ⅰ)证明:PB∥平面COF;
(Ⅱ)证明:AC⊥PD.
分析 由题意可得四边形ABCD是等腰梯形形,四边形ADCO,DOBC都是以半径为边长的菱形,
(Ⅰ)连接BD交OC于H,则H是BD中点,连接FH,即FH∥PB,可得PB∥平面COF
(Ⅱ)由四边形ADCO是以半径为边长的菱形,可得AC⊥CO,及PO⊥AC,可得AC⊥面POD,即可证AC⊥PD
解答 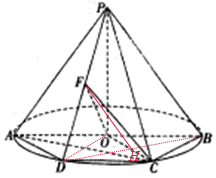 解:如图所示,∵AB是圆O的直径,∴△ABC是直角△,又,∠ABC=60°.
解:如图所示,∵AB是圆O的直径,∴△ABC是直角△,又,∠ABC=60°.
∴BC=$\frac{1}{2}AB$,又∵四边形ABCD是圆的内接四边形,∴四边形ABCD是等腰梯形形,
∴四边形ADCO,DOBC都是以半径为边长的菱形,
(Ⅰ)连接BD交OC于H,则H是BD中点,连接FH,
因为F为PD中点,∴FH∥PB,且PB?面COF,FH?平面COF
∴PB∥平面COF
(Ⅱ)∵四边形ADCO是以半径为边长的菱形
∴AC⊥CO,
∵PO⊥垂直于圆O所在的平面,∴PO⊥AC,且DO∩PO=O
∴AC⊥面POD,
∵PD?面POD,∴AC⊥PD
点评 考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力 空间想象能力,考查化归与转化思想、数形结合思想,是中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
14.直线m:kx+y+4=0(k∈R) 是圆C:x2+y2+4x-4y+6=0的一条对称轴,过点A(0,k)作斜率为1的直线n,则直线n被圆C所截得的弦长为( )
| A. | $\sqrt{14}$ | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
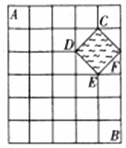 如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.
如图所示,某城镇由6条东西方向的街道和7条南北方向的街道组成,其中有一个池塘,街道在此变成一个菱形的环池大道.现要从城镇的A处走到B处,使所走的路程最短,最多可以有45种不同的走法.