题目内容
设![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且![]() 为它的右准线。
为它的右准线。
(Ⅰ)、求椭圆的方程;
(Ⅱ)、设![]() 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线![]() 分别与椭圆相交于异于
分别与椭圆相交于异于![]() 的点
的点![]() ,证明点
,证明点![]() 在以
在以![]() 为直径的圆内。
为直径的圆内。
(此题不要求在答题卡上画图)
解:(I)依题意得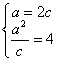 解得
解得![]() 从而
从而![]() ,
,
故椭圆方程为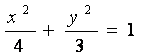 。
。
(II)解法1:由(I)得A(-2,0),B(2,0)。设![]() 。
。
![]() 点在椭圆上,
点在椭圆上,![]() 。
。
又![]() 点异于顶点
点异于顶点![]() ,
,![]()
由![]() 三点共线可得
三点共线可得![]() .
.
从面![]()
![]()
将①式代入②式化简得![]()
![]() ,
,![]() .于是
.于是![]() 为锐角,从而
为锐角,从而![]() 为钝角,故点
为钝角,故点![]() 在以
在以![]() 为直径的圆内.
为直径的圆内.
解法2:由(Ⅰ)得A(-2,0),B(2,0).设P(4,![]() )(
)(![]()
![]() 0),M(
0),M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),则直线AP的方程为
),则直线AP的方程为![]() ,直线BP的方程为
,直线BP的方程为![]() 。
。
![]() 点M、N分别在直线AP、BP上,
点M、N分别在直线AP、BP上,
![]()
![]() ,
,![]() .从而
.从而![]() .③
.③
联立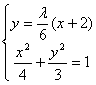 消去
消去![]() 得
得![]() .
.
![]() 是方程得两根,∴(-2).
是方程得两根,∴(-2).![]() ,即
,即![]() . ④
. ④
又![]() . ⑤
. ⑤
于是由③、④式代入⑤式化简可得
![]() .
.
![]() N点在椭圆上,且异于顶点A、B,
N点在椭圆上,且异于顶点A、B,![]()
![]() .
.
又![]() ,
,![]() , 从而
, 从而![]() .
.
故![]() 为钝角,即点B在以MN为直径的圆内.
为钝角,即点B在以MN为直径的圆内.
解法3:由(Ⅰ)得A(-2,0),B(2,0).设M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),则-2<
),则-2<![]() <2 , -2<
<2 , -2<![]() <2.又MN的中点Q的坐标为
<2.又MN的中点Q的坐标为![]() ,
,
![]()
化简得![]() . ⑥
. ⑥
直线AP的方程为![]() ,直线BP的方程为
,直线BP的方程为![]() .
.
![]() 点P在准线
点P在准线![]() 上,
上,
![]()
![]() ,即
,即![]() . ⑦
. ⑦
又![]() M点在椭圆上,
M点在椭圆上,![]() ,即
,即![]() ⑧
⑧
于是将⑦、⑧式化简可得![]() .
.
从而B在以MN为直径的圆内.

练习册系列答案
相关题目
 分别为椭圆
分别为椭圆 的左、右焦点,点A,B在椭圆上,若
的左、右焦点,点A,B在椭圆上,若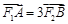 ,
, B.
B. C.
C.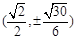 D.
D.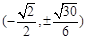
 分别为椭圆
分别为椭圆 的左、右顶点,若在椭圆上存在异于
的左、右顶点,若在椭圆上存在异于 ,使得
,使得 ,其中
,其中 为坐标原点,则椭圆的离心率
为坐标原点,则椭圆的离心率 的取值范围是
的取值范围是  B.
B. C.
C.
 D.
D.
 ,
, 分别为椭圆
分别为椭圆
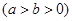 的左、右焦点,过
的左、右焦点,过 与椭圆
与椭圆 相交于
相交于 ,
, 两点,直线
两点,直线 ,
, .
. ,求椭圆
,求椭圆 分别为椭圆
分别为椭圆 的左、右焦点,点
的左、右焦点,点 在椭圆上,若
在椭圆上,若 ;则点
;则点 的坐标是
______.
的坐标是
______. 分别为椭圆
分别为椭圆 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且 为它的右准线.
为它的右准线. 为右准线上不同于点(4,0)的任意一点,若直线
为右准线上不同于点(4,0)的任意一点,若直线 分别与椭圆相交于异于
分别与椭圆相交于异于 ,证明点
,证明点 在以
在以 为直径的圆内.
为直径的圆内.