题目内容

已知A，B为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）上两动点，F1，F2分别为其左右焦点，直线AB过点F2（c，0），且不垂直于x轴，△ABF1的周长为8，且椭圆的短轴长为2
3
．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知点P为椭圆C的左端点，连接PA并延长交直线l：x=4于点M．求证：直线BM过定点．
考点：直线与圆锥曲线的综合问题,椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：（Ⅰ）利用已知条件以及椭圆的定义，求出a，b，即可求椭圆C的标准方程；
（Ⅱ）设直线PA：x=m1y-2，由
x=m1y-2
x2
4
+
y2
3
=1
求出A的坐标，同理求出B的坐标，由A，F2，B三点共线化简A、B坐标，求出M坐标以及BM的方程，利用直线系得到定点坐标，
解答： （本小题满分（12分），（Ⅰ）小问（4分），（Ⅱ）小问8分）
解：（Ⅰ）依题意有：
4a=8
2b=2
3
⇒
a=2
b=
3
，
则椭圆C的方程为
x2
4
+
y2
3
=1…（4分）
（Ⅱ）由椭圆方程可知P（-2，0），F2（1，0），点A（x1，y1），B（x2，y2）
设直线PA：x=m1y-2，由
x=m1y-2
x2
4
+
y2
3
=1
得(3
m
2
1
+4)y2-12m1y=0，从而y1=
12m1
3
m
2
1
+4
，x1=m1y1-2=
6
m
2
1
-8
3
m
2
1
+4
，即点A(
6
m
2
1
-8
3
m
2
1
+4
，
12m1
3
m
2
1
+4
)
同理设直线PB：x=m2y-2，可得B(
6
m
2
2
-8
3
m
2
2
+4
，
12m2
3
m
2
2
+4
)…（7分）
由A，F2，B三点共线可得kAF2=kBF2，即
y1
x1-1
=
y2
x2-1
，代入A，B两点坐标化简可得
m1
m
2
1
-4
=
m2
m
2
2
-4
⇒(m1-m2)(m1m2+4)=0⇒m1m2+4=0…（9分）
直线l：x=4，可得点M(4，
6
m1
)，即M(4，-
3
2
m2)
从而直线BM的方程为y=
12m2
3
m
2
2
+4
+
3
2
m2
6
m
2
2
-8
3
m
2
2
+4
-4
(x-4)-
3
2
m2
化简得y=-
3
4
m2(x-4)-
3
2
m2，即y=-
3
4
m2(x-2)，
从而直线BM过定点（2，0）．…（12分）
点评：本题考查直线与椭圆的位置关系，直线系方程的应用，椭圆的标准方程的求法，考查分析问题解决问题的能力．
练习册系列答案
相关题目
如图，已知P是正方形ABCD平面外一点，M、N分别是PA、BD上的点，且PM：MA=BN：ND=5：8．
求证：直线MN∥平面PBC．
已知函数f（x）=x-1+
a
ex
（a∈R，e为自然对数的底数）．
（Ⅰ）若曲线y=f（x）在点（1，f（1））处的切线平行于x轴，求a；
（Ⅱ）求f（x）的极值．
3名教师与4名学生排成一横排照相，求
（1）3名教师必须排在一起的不同排法有多少种？
（2）3名教师必须在中间（在3、4、5位置上）的不同排法有多少种？
（3）3名教师不能相邻的不同排法有多少种？
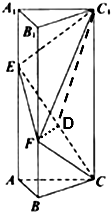如图，已知正三棱柱ABC-A1B1C1的底面边长为2，侧棱长为3
2
，点E在侧棱AA1上，点F在侧棱BB1上，D为线段CE上任意一点，且AE=2
2
，BF=
2
．
（I） 求证：C1E⊥FD；
（Ⅱ） 若D为线段CE的中点，求二面角C1-FD-E的余弦值的大小．
在△ABC中，a，b，c分别为角A，B，C的对边，a=3，b=2
6
，B=2A．
（Ⅰ）求cosA的值； 
（Ⅱ）求边长c的值．
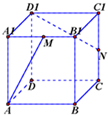如图，正方体ABCD-A1B1C1D1中，M、N分别为A1B1、CC1的中点，求异面直线AM和D1N所成角
 
．
已知圆的内接四边形ABCD中，AB=2，BC=6，AD=CD=4，则四边形ABCD的外接圆半径R的值为
 
．
把一个正方形等分成九个相等的小正方形，将中间的一个正方形挖掉如图（1）；再将剩余的每个正方形都分成九个相等的小正方形，并将中间一个挖掉，得图（2）；如此继续下去…，第三个图中共挖掉
 
个正方形；第n个图中被挖掉的所有小正方形个数为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网