题目内容
在平面直角坐标系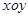 中,曲线
中,曲线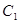 的参数方程为
的参数方程为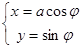 (
(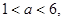
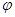 为参数),在以原点
为参数),在以原点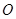 为极点,
为极点,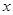 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线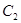 的极坐标方程为
的极坐标方程为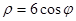 ,射线
,射线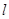 的方程为
的方程为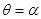 ,又
,又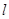 与
与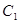 的交点为
的交点为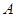 ,
,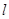 与
与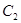 的除极点外的另一个交点为
的除极点外的另一个交点为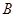 ,当
,当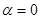 时,
时,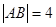 .
.
(1)求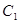 的普通方程,
的普通方程,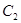 的直角坐标方程;
的直角坐标方程;
(2)设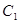 与
与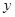 轴正半轴的交点为
轴正半轴的交点为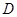 ,当
,当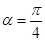 时,求直线
时,求直线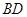 的参数方程.
的参数方程.
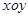 中,曲线
中,曲线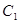 的参数方程为
的参数方程为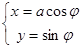 (
(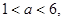
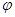 为参数),在以原点
为参数),在以原点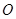 为极点,
为极点,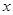 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线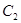 的极坐标方程为
的极坐标方程为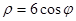 ,射线
,射线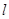 的方程为
的方程为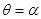 ,又
,又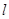 与
与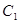 的交点为
的交点为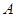 ,
,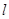 与
与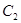 的除极点外的另一个交点为
的除极点外的另一个交点为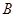 ,当
,当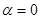 时,
时,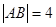 .
.(1)求
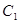 的普通方程,
的普通方程,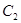 的直角坐标方程;
的直角坐标方程;(2)设
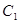 与
与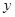 轴正半轴的交点为
轴正半轴的交点为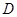 ,当
,当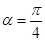 时,求直线
时,求直线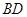 的参数方程.
的参数方程.(1)x2+y2-6x=0.
(2)

(2)

试题分析:解:(Ⅰ)曲线C2的极坐标方程为ρ=6cosφ可化为ρ2=6ρcosφ,
直角坐标方程为x2+y2-6x=0.
曲线C1的参数方程为
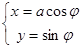 (1<a<6,φ为参数),易消去φ得
(1<a<6,φ为参数),易消去φ得曲线C1的直角坐标方程为

当α=0时,射线l与C1,C2交点的直角坐标分别为(a,0),(6,0),
∵|AB|=4,∴a=2.∴C2直角坐标方程

(Ⅱ)当α=
 时,由x2+ y2-6x=0,y=x得B(3,3)或B(0,0),又B不为极点,∴B(3,3),由(Ⅰ)得D(0,1)
时,由x2+ y2-6x=0,y=x得B(3,3)或B(0,0),又B不为极点,∴B(3,3),由(Ⅰ)得D(0,1)直线BD的参数方程为x=tcosθ,y=1+tsinθ(t为参数),因为经过B(3,3),∴|DB|=
 ,∴cosθ=
,∴cosθ= ,sinθ=
,sinθ= ∴直线BD的参数方程为
∴直线BD的参数方程为
点评:本题考查极坐标方程、参数方程、直角坐标方程之间的互化、应用.考查了直线、圆、椭圆的基本知识.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 的圆心到直线
的圆心到直线 的距离为 .
的距离为 . 和
和 ,则
,则 、
、 两点间的距离是 .
两点间的距离是 . 
 =2上的点到直线
=2上的点到直线 =3的距离的最小值是
=3的距离的最小值是  的直线
的直线 与极轴的夹角
与极轴的夹角 ,若将
,若将 的形式,则
的形式,则

 与直线
与直线 平行,则常数
平行,则常数 的值为_______.
的值为_______.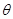 )(
)(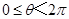 )中,曲线
)中,曲线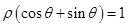 与
与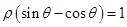 的交点的极坐标为 .
的交点的极坐标为 . 的位置关系是 _
的位置关系是 _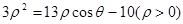
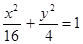 ,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值.
,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值.