题目内容
直线xcosα+y+b=0(α、b∈R)的倾斜角范围是________.
[0, ]∪[
]∪[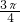 ,π]
,π]
分析:由题意可得直线的斜率为-cosα,设直线xcosα+y+b=0(α、b∈R)的倾斜角是θ,则-1≤tanθ≤1,由此求得倾斜角θ的范围.
解答:直线xcosα+y+b=0(α、b∈R)的斜率为-cosα,
∵-1≤cosα≤1,
∴-1≤-cosα≤1.
设直线xcosα+y+b=0(α、b∈R)的倾斜角是θ,则-1≤tanθ≤1.
再由 0≤θ<π,可得 θ∈[0, ]∪[
]∪[ ,π],
,π],
故答案为[0, ]∪[
]∪[ ,π].
,π].
点评:本题主要考查直线的倾斜角和斜率的关系,以及倾斜角的取值范围,已知三角函数值求角的大小,属于基础题.
 ]∪[
]∪[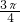 ,π]
,π]分析:由题意可得直线的斜率为-cosα,设直线xcosα+y+b=0(α、b∈R)的倾斜角是θ,则-1≤tanθ≤1,由此求得倾斜角θ的范围.
解答:直线xcosα+y+b=0(α、b∈R)的斜率为-cosα,
∵-1≤cosα≤1,
∴-1≤-cosα≤1.
设直线xcosα+y+b=0(α、b∈R)的倾斜角是θ,则-1≤tanθ≤1.
再由 0≤θ<π,可得 θ∈[0,
 ]∪[
]∪[ ,π],
,π],故答案为[0,
 ]∪[
]∪[ ,π].
,π].点评:本题主要考查直线的倾斜角和斜率的关系,以及倾斜角的取值范围,已知三角函数值求角的大小,属于基础题.

练习册系列答案
相关题目
直线xcosθ+y-1=0(θ∈R)的倾斜角的范围是( )
| A、[0,π) | ||||
B、[0,
| ||||
C、(-
| ||||
D、(0,
|