题目内容
20.给定两个命题,命题p:对任意实数x都有ax2>-ax-1恒成立,命题q:关于x的方程x2-x+a=0有实数根.若“p或q”为真命题,“p且q”为假命题,求实数a的取值范围.分析 因为“p或q”为真命题,“p且q”为假命题,所以p,q中有且仅有一个为真命题.进而可得实数a的取值范围.
解答 解:若p为真命题,则a=0或$\left\{\begin{array}{l}a>0\\{a}^{2}-4a<0\end{array}\right.$.
即0≤a<4;
若q为真命题,则(-1)2-4a≥0,即a≤$\frac{1}{4}$.
因为“p或q”为真命题,“p且q”为假命题,
所以p,q中有且仅有一个为真命题.
若p真q假,则$\frac{1}{4}$<a<4;
若p假q真,则a<0.
综上,实数a的取值范围为(-∞,0)∪($\frac{1}{4}$,4).
点评 本题以命题的真假判断与应用为载体,考查了复合命题,函数的恒成立问题,方程根的存在性及个数判断等知识点,难度中档.

练习册系列答案
相关题目
11.已知i为虚数单位,则复数$\frac{1+i}{i}$=( )
| A. | 1+i | B. | 1-i | C. | 1+$\frac{i}{2}$ | D. | 1-$\frac{i}{2}$ |
8.已知点P位椭圆C:$\frac{x^2}{4}+\frac{y^2}{9}=1$上任意一点,则P到直线l:2x-y=12的距离的最小值为( )
| A. | $\frac{7}{5}$ | B. | $\frac{7}{5}\sqrt{5}$ | C. | $\frac{17}{5}$ | D. | $\frac{17}{5}\sqrt{5}$ |
9.《庄子•天下篇》中记述了一个著名命题:“一尺之锤,日取其半,万世不竭”.反映这个命题本质的式子是( )
| A. | 1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=2-$\frac{1}{{2}^{n}}$ | B. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$<1 | ||
| C. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$=1 | D. | $\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$>1 |

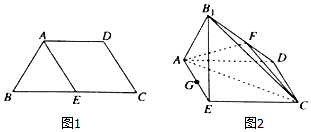 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面ABCD,F,G分别为B1D,AE的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面ABCD,F,G分别为B1D,AE的中点.