题目内容
已知tan((1)tanα的值;
(2)![]() 的值.
的值.
思路分析:(1)利用两角和的正切公式易求得tanα的值.
(2)思路一:将sin2α、cos2α转化为α的单角形式,然后分子、分母同除以cos2α,使表达式中只含tanα,再利用(1)中结果即可求得.
思路二:利用(1)中的结果可得出sinα与cosα的一个等量关系,又sin2α+cos2α=1,从而可求得cos2α的值,而cos2α=2cos2α-1,sin2α=2sinαcosα,所以sin2α、cos2α的值也可求出.
(1)解:tan(![]() +α)=
+α)= =
=![]() ,
,
由tan(![]() +α)=
+α)=![]() 得
得![]() =
=![]() ,
,
解得tanα=-![]() .
.
(2)解法一:![]() =
=![]() =tanα-
=tanα-![]() =-
=-![]() -
-![]() =-
=-![]() .
.
解法二:由(1)知tanα=-![]() ,
,
得sinα=-![]() cosα,
cosα,
所以sin2α=![]() cos2α.
cos2α.
又sin2α+cos2α=1,
所以![]() cos2α+cos2α=1,即cos2α=
cos2α+cos2α=1,即cos2α=![]() .
.
于是cos2α=2cos2α-1=2×![]() -1=
-1=![]() ,sin2α=2sinα·cosα=-
,sin2α=2sinα·cosα=-![]() cos2α=-
cos2α=-![]() ,
,
故![]() =
=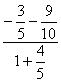 =-
=-![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
已知tan(θ+
)=-3,则sin2θ+sinθcosθ-2cos2θ=( )
| π |
| 4 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|