题目内容
16.若抛物线y2=4x上仅存在3个不同的点到直线x-y+m=0的距离为$\sqrt{2}$,则m的值为( )| A. | 1 | B. | -1 | C. | -2或3 | D. | -1或3 |
分析 到直线x-y+m=0的距离为$\sqrt{2}$的点的轨迹为两条平行直线x-y+m±2=0,当这两条直线一条与抛物线与抛物线相切时,令一条与抛物线相交时满足题意,联立方程组,求出m的值,再讨论即可求出
解答 解:到直线x-y+m=0的距离为$\sqrt{2}$的点的轨迹为两条平行直线x-y+m±2=0,
当这两条直线一条与抛物线与抛物线相切时,令一条与抛物线相交时满足题意,
将x-y+m±2=0与y2=4x联立得y2-4y+4m±8=0,
由△=0,即16-4(4m±8)=0,
可得m=-1,3,
当m=3时,两条平行线y+m±2=0一条与抛物线相切,另一条与抛物线相离,
当m=-1时,两条平行线y+m±2=0一条与抛物线相切,另一条与抛物线相交,
故选:B
点评 本题考查了直线和抛物线的位置关系,考查了转化能力和运算能力,属于中档题.

练习册系列答案
相关题目
7.已知某同学在高二期末考试中,A和B两道选择题同时答对的概率为$\frac{2}{3}$,在A题答对的情况下,B题也答对的概率为$\frac{8}{9}$,则A题答对的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{9}$ |
11.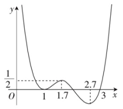 函数f(x)的图象如图所示,则f(x)的极大值点为( )
函数f(x)的图象如图所示,则f(x)的极大值点为( )
 函数f(x)的图象如图所示,则f(x)的极大值点为( )
函数f(x)的图象如图所示,则f(x)的极大值点为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 1.7 | D. | 2.7 |
5.设全集U={1,2,3,4,5,6},A={1,3,5},B={2,3},则(∁UA)∪B=( )
| A. | {2,3,4,6} | B. | {2,3} | C. | {1,2,3,5} | D. | {2,4,6} |