题目内容
7.设函数f(x)=px-$\frac{p}{x}$-2lnx.(Ⅰ)若p=1,函数y=f(x)是否有极值,若有,请求出极值,若没有,请说明理由.
(Ⅱ)若f(x)在其定义域内为单调函数,求实数p的取值范围.
分析 (Ⅰ)把p=1代入确定出函数y=f(x)解析式,求出导函数,即可做出判断;
(Ⅱ)求出f(x)导函数f′(x)=$\frac{1}{{x}^{2}}$(px2-2x+p),以及定义域,设h(x)=px2-2x+p,要使y=f(x)在(0,+∞)单调,只需h(x)≥0或h(x)≤0恒成立,分p<0,p=0,p>0三种情况求出p的范围即可.
解答 解:(Ⅰ)把p=1代入得:f(x)=x-$\frac{1}{x}$-2lnx,
∴f′(x)=1+$\frac{1}{{x}^{2}}$-$\frac{2}{x}$=($\frac{1}{x}$-1)2≥0,
∴函数y=f(x)没有极值;
(Ⅱ)f′(x)=$\frac{1}{{x}^{2}}$(px2-2x+p),定义域为(0,+∞),
令h(x)=px2-2x+p,
要使y=f(x)在(0,+∞)单调,只需h(x)≥0或h(x)≤0恒成立,
当p=0时,h(x)=-2x,此时f′(x)<0,函数y=f(x)在(0,+∞)单调递减;
当p>0时,h(x)min=h($\frac{1}{p}$)≥0,即p-$\frac{1}{p}$≥0,
解得:p≥1;
当p<0时,h(x)在(0,+∞)上单调递减,又h(0)=p<0,满足题意,
综上,实数p的取值范围是p≥1或p≤0.
点评 此题考查了利用导数研究函数的极值,利用导数研究函数的单调性,熟练掌握导函数的性质是解本题的关键.

练习册系列答案
相关题目
17.已知函数y=$\left\{{\begin{array}{l}{{x^2}+1}\\{-2x}\end{array}}$$\begin{array}{l}{(x>0)}\\{(x<0)}\end{array}$,使函数值为5的x的值是( )
| A. | -2 | B. | 2或$-\frac{5}{2}$ | C. | 2或-2 | D. | 2或-2或$-\frac{5}{2}$ |
19.一个几何体的三视图如图所示,则这个几何体的表面积为( )

| A. | 22+$\frac{2}{3}$π | B. | 22+$\frac{5}{3}$π | C. | 22+$\frac{8}{3}$π | D. | 22-π |
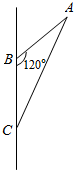 如图所示,在△ABC中,AB=2,BC=2,∠ABC=120°,若将△ABC绕BC旋转一周,求所形成的旋转体的表面积和体积.
如图所示,在△ABC中,AB=2,BC=2,∠ABC=120°,若将△ABC绕BC旋转一周,求所形成的旋转体的表面积和体积.