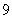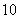题目内容
数列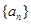 满足
满足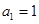 ,
,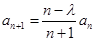 ,其中
,其中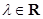 ,
,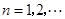 .
.
①当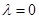 时,
时,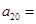 _____;
_____;
②若存在正整数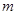 ,当
,当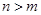 时总有
时总有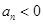 ,则
,则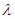 的取值范围是_____.
的取值范围是_____.
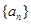 满足
满足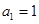 ,
,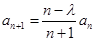 ,其中
,其中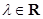 ,
,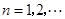 .
.①当
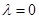 时,
时,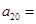 _____;
_____;②若存在正整数
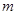 ,当
,当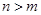 时总有
时总有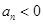 ,则
,则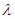 的取值范围是_____.
的取值范围是_____..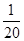 ;
; .
.
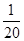 ;
; .
.①当λ=0时,an+1=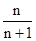 an,利用累积法求通项公式后,再求a20即可.
an,利用累积法求通项公式后,再求a20即可.
②记bn=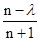 (n=1,2,…),则λ满足
(n=1,2,…),则λ满足
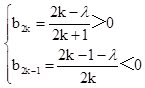 .由此可求出故λ的取值范围.
.由此可求出故λ的取值范围.
解答:解:①当λ=0时,
an+1=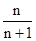 an,
an,
∴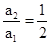
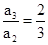
…
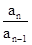 =
=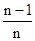
以上各式相乘得出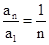
又a1=1,
∴an=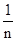 .
.
a20=1/20
②记bn=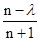 (n=1,2,),根据题意可知,且λ≠n(n∈N*),这时总存在n0∈N*,满足:当n≥n0时,bn>0;
(n=1,2,),根据题意可知,且λ≠n(n∈N*),这时总存在n0∈N*,满足:当n≥n0时,bn>0;
当n≤n0-1时,bn<0.所以由an+1=bnan及a1=1>0可知,若n0为偶数,
则an0<0,从而当n>n0时,an<0;若n0为奇数,则an0>0,
从而当n>n0时an>0.因此“存在m∈N*,当n>m时总有an<0”
的充分必要条件是:n0为偶数,
记n0=2k(k=1,2,),则λ满足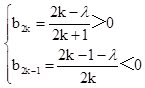 .
.
故λ的取值范围是λ∈(2k-1,2k),
故答案为:1/20,(2k-1,2k),(k=1,2,),
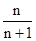 an,利用累积法求通项公式后,再求a20即可.
an,利用累积法求通项公式后,再求a20即可.②记bn=
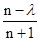 (n=1,2,…),则λ满足
(n=1,2,…),则λ满足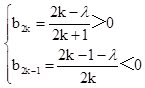 .由此可求出故λ的取值范围.
.由此可求出故λ的取值范围.解答:解:①当λ=0时,
an+1=
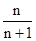 an,
an,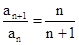
∴
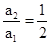
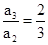
…
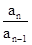 =
=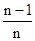
以上各式相乘得出
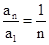
又a1=1,
∴an=
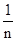 .
.a20=1/20
②记bn=
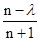 (n=1,2,),根据题意可知,且λ≠n(n∈N*),这时总存在n0∈N*,满足:当n≥n0时,bn>0;
(n=1,2,),根据题意可知,且λ≠n(n∈N*),这时总存在n0∈N*,满足:当n≥n0时,bn>0;当n≤n0-1时,bn<0.所以由an+1=bnan及a1=1>0可知,若n0为偶数,
则an0<0,从而当n>n0时,an<0;若n0为奇数,则an0>0,
从而当n>n0时an>0.因此“存在m∈N*,当n>m时总有an<0”
的充分必要条件是:n0为偶数,
记n0=2k(k=1,2,),则λ满足
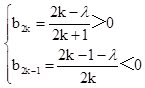 .
.故λ的取值范围是λ∈(2k-1,2k),
故答案为:1/20,(2k-1,2k),(k=1,2,),

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
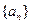 的前
的前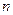 项和为
项和为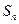 ,
,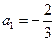 ,且
,且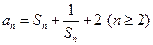 .
.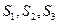 ;
;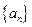 满足
满足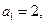 前
前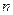 项和为
项和为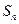 ,
,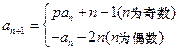 .
.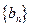 满足
满足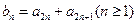 ,试求数列
,试求数列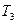 ;(4分)
;(4分)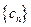 满足
满足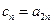 ,试判断
,试判断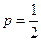 时,问是否存在
时,问是否存在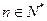 ,使得
,使得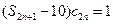 ,若存在,求出所有的
,若存在,求出所有的 中,
中, 的值是
的值是  为等差数列,且
为等差数列,且 ,
, 为等比数列,数列
为等比数列,数列 前三项依次为5,11,21.
前三项依次为5,11,21. 的通项公式;
的通项公式;  项和
项和 .
. , 则数列的通项
, 则数列的通项 =__
=__  满足:
满足: 是公差为1的等差数列,且
是公差为1的等差数列,且
 ;
; ,求证:
,求证:
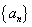 满足
满足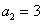 ,
,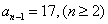 ,
, ,则
,则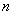 的值为( )
的值为( )