题目内容
已知( +
+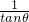 )•
)• =2,求
=2,求 的值.
的值.
解:已知( +
+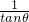 )•
)• =(
=( +
+ )•
)•
= •
• =
= =
= =
= =tanθ,即tanθ=2
=tanθ,即tanθ=2
又 =
= =
= =
=
将tanθ=2代入得:原式= =1
=1
分析:把已知条件通分并利用同角三角函数间的基本关系化简得到tanθ的值,然后把所求的式子也利用同角三角函数间的基本关系化简得到关于tanθ的式子,把tanθ的值代入即可求出.
点评:考查学生灵活运用同角三角函数间的基本关系化简求值.解题的思路是将已知和所求都化为正切.
 +
+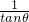 )•
)• =(
=( +
+ )•
)•
=
 •
• =
= =
= =
= =tanθ,即tanθ=2
=tanθ,即tanθ=2又
 =
= =
= =
=
将tanθ=2代入得:原式=
 =1
=1分析:把已知条件通分并利用同角三角函数间的基本关系化简得到tanθ的值,然后把所求的式子也利用同角三角函数间的基本关系化简得到关于tanθ的式子,把tanθ的值代入即可求出.
点评:考查学生灵活运用同角三角函数间的基本关系化简求值.解题的思路是将已知和所求都化为正切.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目