题目内容
抛物线的顶点在原点，对称轴为y轴，它与圆x2＋y2＝9相交，公共弦MN的长为2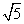
，求该抛物线的方程，并写出它的焦点坐标与准线方程．
解 由题意，抛物线方程为x2＝2ay(a≠0)．
设公共弦MN交y轴于A，则MA＝AN，而AN＝.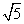
∵ON＝3，∴OA＝ 
＝2，
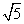∴N(，±2)．
∵N点在抛物线上，∴5＝2a·(±2)，即2a＝±
，
故抛物线的方程为x2＝y或x2＝－y.
抛物线x2＝±y的焦点坐标为
，
准线方程为y＝∓
.
练习册系列答案
相关题目
＋
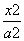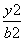＝1(a>b>0)的左、右焦点，顶点B的坐标为(0，b)，连接BF2并延长交椭圆于点A，过点A作x轴的垂线交椭圆于另一点C，连接F1C.
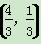，且BF2＝
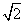，求椭圆的方程；
－
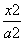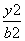＝1(a>0，b>0)的离心率为2，A，B为其左，右顶点，点P为双曲线C在第一象限的任意一点，点O为坐标原点，若PA，PB，PO的斜率为k1，k2，k3，则m＝k1k2k3的取值范围为( )
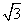) B．(0，
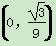D．(0,8)
则|QF|＝( )
B．3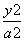
＋
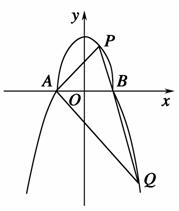
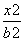＝1(a>b>0，y≥0)和部分抛物线C2：y＝－x2＋1(y≤0)连接而成，C1与C2的公共点为A，B，其中C1的离心率为
.
－
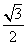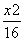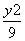＝1的左、右焦点的距离之比为23，则点M的轨迹方程为____________________．
－
＝1与直线x＋y－1＝0相交于P，Q两点，且
＝0(O为原点)，则
－
的值为________．