题目内容
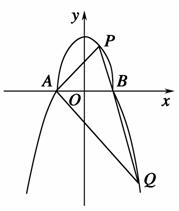
如图,曲线C由上半椭圆C1: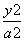 +
+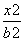 =1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为
=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为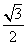 .
.
(1)求a,b的值;
(2)过点B的直线l与C1,C2分别交于点P,Q(均异于点A,B),若AP⊥AQ,求直线l的方程.
解 (1)在C1,C2的方程中,令y=0,可得b=1,且A(-1,0),B(1,0)是上半椭圆C1的左右顶点.
设C1的半焦距为c,由 =
=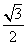 及a2-c2=b2=1得a=2.∴a=2,b=1.
及a2-c2=b2=1得a=2.∴a=2,b=1.
(2)由(1)知,上半椭圆C1的方程为 +x2=1(y≥0).
+x2=1(y≥0).
易知,直线l与x轴不重合也不垂直,设其方程为y=k(x-1)(k≠0),
代入C1的方程,整理得(k2+4)x2-2k2x+k2-4=0.(*)
设点P的坐标为(xP,yP),
∵直线l过点B,∴x=1是方程(*)的一个根,
 ∵k≠0,∴k-4(k+2)=0,解得k=-
∵k≠0,∴k-4(k+2)=0,解得k=- .
.
经检验,k=- 符合题意,
符合题意,
故直线l的方程为y=- (x-1),
(x-1),
即8x+3y-8=0.

练习册系列答案
相关题目
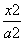 -
- =1(a>0)的离心率为2,则a=( )
=1(a>0)的离心率为2,则a=( )
 D.1
D.1 D.4
D.4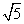 ,求该抛物线的方程,并写出它的焦点坐标与准线方程.
,求该抛物线的方程,并写出它的焦点坐标与准线方程.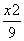 -
- =1
=1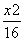 -
-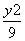 =1
=1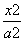 +
+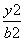 =1(a>b>0)经过点M
=1(a>b>0)经过点M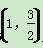 ,其离心率为
,其离心率为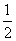 .
.