题目内容
如图,在平面直角坐标系xOy中,F1,F2分别是椭圆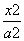 +
+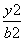 =1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.
=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.
(1)若点C的坐标为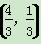 ,且BF2=
,且BF2=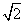 ,求椭圆的方程;
,求椭圆的方程;
(2)若F1C⊥AB,求椭圆离心率e的值.
解 设椭圆的焦距为2c,则F1(-c,0),F2(c,0).
(1)因为B(0,b),所以BF2= =a.
=a.
又BF2=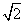 ,故a=
,故a=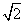 .
.
因为点 解得b2=1.
解得b2=1.
故所求椭圆的方程为 +y2=1.
+y2=1.
(2)因为B(0,b),F2(c,0)在直线AB上,
所以直线AB的方程为 +
+ =1.
=1.
解方程组
 所以点A的坐标为
所以点A的坐标为 .
.
又AC垂直于x轴,由椭圆的对称性,可得点C的坐标为
因为直线F1C的斜率为 ,直线AB的斜率为-
,直线AB的斜率为- ,且F1C⊥AB,
,且F1C⊥AB,
 又b2=a2-c2,整理得a2=5c2.故e2=
又b2=a2-c2,整理得a2=5c2.故e2= .
.
因此e= .
.

练习册系列答案
相关题目
 B.-
B.- D.
D.
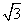 D.3
D.3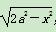 ,a>0},N={(x,y)|(x-1)2+(y-
,a>0},N={(x,y)|(x-1)2+(y-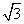 )2=a2,a>0},则M∩N≠∅时,a的最大值与最小值分别为________、________.
)2=a2,a>0},则M∩N≠∅时,a的最大值与最小值分别为________、________.

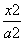 -
- =1(a>0)的离心率为2,则a=( )
=1(a>0)的离心率为2,则a=( )
 D.1
D.1 -
- =1的离心率为
=1的离心率为 ,则m等于________.
,则m等于________.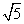 ,求该抛物线的方程,并写出它的焦点坐标与准线方程.
,求该抛物线的方程,并写出它的焦点坐标与准线方程.