题目内容
4.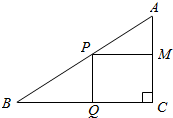 直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?
直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?
分析 先表示出矩形PQCM的面积,再利用基本不等式,即可得出结论.
解答 解:设PM=xcm,PQ=ycm,则$\frac{x}{4}=\frac{3-y}{3}$,∴y=3-$\frac{3}{4}$x,
∴矩形PQCM的面积S=xy=x(3-$\frac{3}{4}$x)=$\frac{4}{3}$•$\frac{3}{4}$x(3-$\frac{3}{4}$x)≤$\frac{4}{3}•\frac{9}{4}$=3,
当且仅当$\frac{3}{4}$x=1-$\frac{3}{4}$x,即x=$\frac{2}{3}$时,矩形PQCM的面积最大,最大面积是4,
此时,AP:AB=1:6.
点评 本题考查比例线段,考查矩形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
16.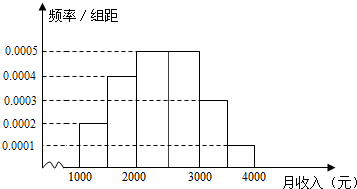 某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )
某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )
 某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )
某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )| A. | 2360 | B. | 2380 | C. | 2400 | D. | 2420 |
14.用配方法解方程x2+4x+1=0,配方后的方程是( )
| A. | (x+2)2=3 | B. | (x-2)2=3 | C. | (x-2)2=5 | D. | (x+2)2=5 |
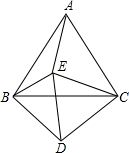 如图,设△ABC和△CDE都是等边三角形,且∠EBD=62°,则∠AEB的度数为122°.
如图,设△ABC和△CDE都是等边三角形,且∠EBD=62°,则∠AEB的度数为122°.
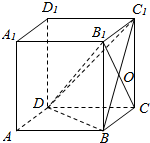 如图,边长为2的正方体ABCD-A1B1C1D1中,B1C与BC1相交于点O.
如图,边长为2的正方体ABCD-A1B1C1D1中,B1C与BC1相交于点O.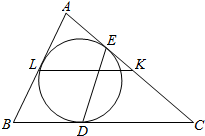 如图,己知L、K分别是△ABC的边AB、AC的中点.△ABC的内切圆⊙l分别与边BC、CA切于点D、E.求证:KL、DE的交点在∠ABC的角平分线上.
如图,己知L、K分别是△ABC的边AB、AC的中点.△ABC的内切圆⊙l分别与边BC、CA切于点D、E.求证:KL、DE的交点在∠ABC的角平分线上.