题目内容
14.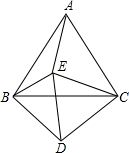 如图,设△ABC和△CDE都是等边三角形,且∠EBD=62°,则∠AEB的度数为122°.
如图,设△ABC和△CDE都是等边三角形,且∠EBD=62°,则∠AEB的度数为122°.
分析 由已知条件推导出△ACE≌△BCD,从而∠DBC=∠CAE,再通过角之间的转化,利用三角形内角和定理能求出∠AEB的度数.
解答 解:∵△ABC和△CDE都是等边三角形,且∠EBD=62°,
∴AC=BC,CE=CD,∠ACB=∠ECD=60°,
又∵∠ACB=∠ACE+∠BCE,∠ECD=∠BCE+∠BCD,
∴∠BCD=∠ACE,△ACE≌△BCD,
∴∠DBC=∠CAE,
∴62°-∠EBC=60°-∠BAE,
∴62°-(60°-∠ABE)=60°-∠BAE,
∴∠AEB=180°-(∠ABE+∠BAE)=180°-58°=122°.
故答案为:122°.
点评 本题考查角的大小的求法,是基础题,解题时要注意等边三角形的性质、三角形全等的性质和三角形内角和定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.双曲线$\frac{{x}^{2}}{25-k}$+$\frac{{y}^{2}}{9-k}$=1的焦距为( )
| A. | 16 | B. | 8 | ||
| C. | 4 | D. | 不确定,与k值有关 |
6.已知正实数a、b、c满足$\frac{1}{e}≤\frac{c}{a}$≤2,clnb=a+clnc,其中e是自然对数的底数,则ln$\frac{b}{a}$的取值范围是( )
| A. | [1,+∞) | B. | $[{1,\frac{1}{2}+ln2}]$ | C. | (-∞,e-1] | D. | [1,e-1] |
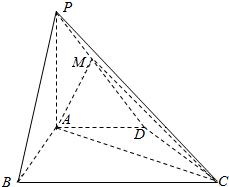 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,∠ABC=60°,AB=AD=2,PA=BC=4,M是PD的中点.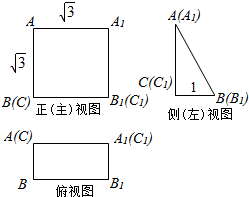 一个空间几何体的三视图及部分数据如图所示.
一个空间几何体的三视图及部分数据如图所示. 如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
如图,圆O的直径AB=10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.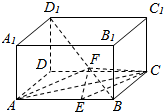 如图,在长方体ABCD-A1B1C1D1中,AB=3,AA1=AD=2,BE=1,F是BD1上一点,且EF∥平面ADD1A1,则三棱锥E-AFC的体积为$\frac{4}{9}$.
如图,在长方体ABCD-A1B1C1D1中,AB=3,AA1=AD=2,BE=1,F是BD1上一点,且EF∥平面ADD1A1,则三棱锥E-AFC的体积为$\frac{4}{9}$.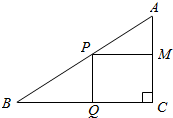 直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?
直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?