题目内容
10. 在棱长为1的正方体ABCD-A1B1C1D1中,E为线段B1C的中点,F是棱C1D1上的动点,若点P为线段BD1上的动点,则PE+PF的最小值为( )
在棱长为1的正方体ABCD-A1B1C1D1中,E为线段B1C的中点,F是棱C1D1上的动点,若点P为线段BD1上的动点,则PE+PF的最小值为( )| A. | $\frac{1+\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{5\sqrt{2}}{6}$ |
分析 连接BC1,得出点P、E、F在平面BC1D1中,问题转化为在平面内直线BD1上取一点P,求点P到定点E的距离与到定直线的距离的和的最小值问题,利用平面直角坐标系,求出点E关于直线BD1的坐标即可.
解答 解:连接BC1,则BC1∩B1C=E,点P、E、F在平面BC1D1中,
且BC1⊥C1D1,C1D1=1,BC1=$\sqrt{2}$,
如图1所示;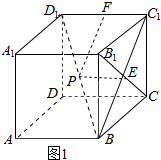
在Rt△BC1D1中,以C1D1为x轴,C1B为y轴,建立平面直角坐标系,
如图2所示;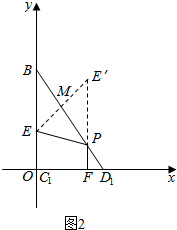
则D1(1,0),B(0,$\sqrt{2}$),E(0,$\frac{\sqrt{2}}{2}$);
设点E关于直线BD1的对称点为E′,
∵BD1的方程为x+$\frac{y}{\sqrt{2}}$=1①,
∴kEE′=-$\frac{1}{-\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴直线EE′的方程为y=$\frac{\sqrt{2}}{2}$x+$\frac{\sqrt{2}}{2}$②,
由①②组成方程组,解得$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{2\sqrt{2}}{3}}\end{array}\right.$,
直线EE′与BD1的交点M($\frac{1}{3}$,$\frac{2\sqrt{2}}{3}$);
所以对称点E′($\frac{2}{3}$,$\frac{5\sqrt{2}}{6}$),
∴PE+PF=PE′+PF≥E′F=$\frac{5\sqrt{2}}{6}$.
故选:D.
点评 本题考查了空间几何体中距离和的计算问题,解题的关键是把空间问题转化为平面问题解答,是难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.当x=$\frac{π}{4}$时,函数f(x)=Asin(x+φ)(A>0)取得最小值,则函数y=f($\frac{3π}{4}$-x)是( )
| A. | 奇函数且图象关于直线x=$\frac{π}{2}$对称 | B. | 偶函数且图象关于点(π,0)对称 | ||
| C. | 奇函数且图象关于($\frac{π}{2}$,0)对称 | D. | 偶函数且图象关于点($\frac{π}{2}$,0)对称 |
18.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x-1}-2,(x≤1)}\\{-lo{g}_{2}(x+1),(x>1)}\end{array}\right.$,则f[f(3)]=( )
| A. | -$\frac{15}{8}$ | B. | -$\frac{15}{4}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{1}{4}$ |
2.设a>0,b>0,则“x>a且y>b”是“x+y>a+b,且xy>ab”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.已知向量$\overline{a}$=(1,-$\sqrt{3}$),$\overline{b}$=(-2,0),则$\overline{a}$与$\overline{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
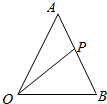 如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.
如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足$\overrightarrow{AP}$=λ$\overrightarrow{PB}$.