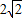题目内容
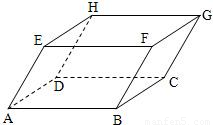
 对于向量a,b,定义a×b为向量a,b的向量积,其运算结果为一个向量,且规定a×b的模|a×b|=|a||b|sinθ(其中θ为向量a与b的夹角),a×b的方向与向量a,b的方向都垂直,且使得a,b,a×b依次构成右手系.如图,在平行六面体ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,AB=AD=AE=2,则(
对于向量a,b,定义a×b为向量a,b的向量积,其运算结果为一个向量,且规定a×b的模|a×b|=|a||b|sinθ(其中θ为向量a与b的夹角),a×b的方向与向量a,b的方向都垂直,且使得a,b,a×b依次构成右手系.如图,在平行六面体ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,AB=AD=AE=2,则(| AB |
| AD |
| AE |
| A、4 | ||
| B、8 | ||
C、2
| ||
D、4
|
分析:根据题意和向量积定义,判断出向量
×
的方向且垂直平面ABCD,由数量积的运算需要求出向量
×
和
所成角θ的余弦值,即由题意作EI⊥AC于I,则<AEI=θ,过I作IJ⊥AD于J,连EJ,由三垂线逆定理可得EJ⊥AD,在直角三角形求出cosθ的值和向量的模,最后代入向量积和数量积定义求解.
| AB |
| AD |
| AB |
| AD |
| AE |
解答: 解:据向量积定义知,向量
解:据向量积定义知,向量
×
垂直平面ABCD,且方向向上,设
×
与
所成角为θ.
∵∠EAB=∠EAD=∠BAD=60°,
∴点E在底面ABCD上的射影在直线AC上.
作EI⊥AC于I,则EI⊥面ABCD,∴θ+∠EAI=
.
过I作IJ⊥AD于J,连EJ,由三垂线逆定理可得EJ⊥AD.
∵AE=2,∠EAD=60°,∴AJ=1,EJ=
.
又∵∠CAD=30°,IJ⊥AD,∴AI=
.
∵AE=2,EI⊥AC,∴cos∠EAI=
=
.
∴sinθ=sin(
-∠EAI)=cos∠EAI=
,cosθ=
.
故(
×
)•
=|
||
|sin∠BAD|
|cosθ=8×
×
=4
,
故选D.
 解:据向量积定义知,向量
解:据向量积定义知,向量| AB |
| AD |
| AB |
| AD |
| AE |
∵∠EAB=∠EAD=∠BAD=60°,
∴点E在底面ABCD上的射影在直线AC上.
作EI⊥AC于I,则EI⊥面ABCD,∴θ+∠EAI=
| π |
| 2 |
过I作IJ⊥AD于J,连EJ,由三垂线逆定理可得EJ⊥AD.
∵AE=2,∠EAD=60°,∴AJ=1,EJ=
| 3 |
又∵∠CAD=30°,IJ⊥AD,∴AI=
2
| ||
| 3 |
∵AE=2,EI⊥AC,∴cos∠EAI=
| AI |
| AE |
| ||
| 3 |
∴sinθ=sin(
| π |
| 2 |
| ||
| 3 |
| ||
| 3 |
故(
| AB |
| AD |
| AE |
| AB |
| AD |
| AE |
| ||
| 2 |
| ||
| 3 |
| 2 |
故选D.
点评:本题是新定义题目,需要抓住新定义中的本质找到解题的关键点,即
×
的方向和具体位置,根据图形和条件作出并加以证明,还需要利用几何知识和向量数量积的运算进行求解,考查分析问题和解决问题的能力.
| AB |
| AD |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 结果为一个向量,且规定a×b的模|a×b|=|a||b|sinθ(其中
结果为一个向量,且规定a×b的模|a×b|=|a||b|sinθ(其中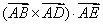 =
( )
=
( )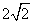 D.
D.
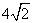
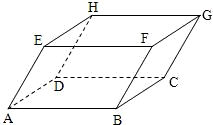 对于向量a,b,定义a×b为向量a,b的向量积,其运算结果为一个向量,且规定a×b的模|a×b|=|a||b|sinθ(其中θ为向量a与b的夹角),a×b的方向与向量a,b的方向都垂直,且使得a,b,a×b依次构成右手系.如图,在平行六面体ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,AB=AD=AE=2,则
对于向量a,b,定义a×b为向量a,b的向量积,其运算结果为一个向量,且规定a×b的模|a×b|=|a||b|sinθ(其中θ为向量a与b的夹角),a×b的方向与向量a,b的方向都垂直,且使得a,b,a×b依次构成右手系.如图,在平行六面体ABCD-EFGH中,∠EAB=∠EAD=∠BAD=60°,AB=AD=AE=2,则 =
=

 =( )
=( )

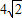
 =( )
=( )