题目内容
已知函数 与函数
与函数 .
.
(I)若 的图象在点
的图象在点 处有公共的切线,求实数
处有公共的切线,求实数 的值;
的值;
(II)设 ,求函数
,求函数 的极值.
的极值.
(I)因为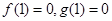 ,
,
所以点 同时在函数
同时在函数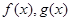 的图象上 …………… 1分
的图象上 …………… 1分
因为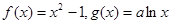 ,
, 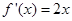 , ……………3分
, ……………3分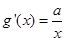 ……………5分
……………5分
由已知,得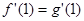 ,所以
,所以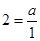 ,即
,即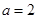 ……………6分
……………6分
(II)因为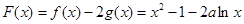 (
(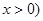 ………7分
………7分
所以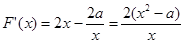 ……………8分
……………8分
当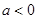 时,
时,
因为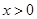 ,且
,且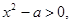 所以
所以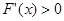 对
对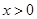 恒成立,
恒成立,
所以 在
在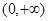 上单调递增,
上单调递增, 无极值 ………10分;
无极值 ………10分;
当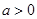 时,
时,
令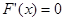 ,解得
,解得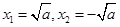 (舍) ………11分
(舍) ………11分
所以当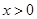 时,
时, 的变化情况如下表:
的变化情况如下表: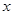
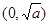
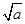
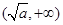
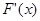
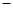
0 + 
递减 极小值 递增
……………13分
所以当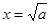 时,
时, 取得极小值,且
取得极小值,且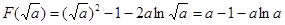 . ……………15分
. ……………15分
综上,当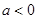 时,函数
时,函数 在
在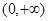 上无极值;
上无极值;
当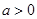 时,函数
时,函数 在
在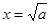 处取得极小值
处取得极小值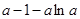 .
.
解析

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
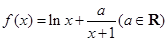 .
.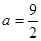 时,求
时,求 的极值;
的极值; 时,试比较
时,试比较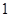 的大小;
的大小;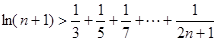 (
(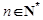 ).
). x2+lnx.
x2+lnx. x3.
x3. ,
,  .
. 在
在 上是单调函数,求
上是单调函数,求 的取值范围;
的取值范围; 在区间
在区间 内有两个不同的零点?若存在,请求出
内有两个不同的零点?若存在,请求出 上的函数
上的函数 ,其中
,其中 为大于零的常数.
为大于零的常数. 时,令
时,令 ,
, 时,
时, (
( 为自然对数的底数);
为自然对数的底数); ,在
,在 处取得最大值,
处取得最大值, 。
。 ,函数
,函数 在
在 上既能取到极大值,又能取到极小值,求
上既能取到极大值,又能取到极小值,求 的取值范围;
的取值范围; 时,
时, 对任意的
对任意的 恒成立,求
恒成立,求 的取值范围;
的取值范围;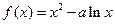 ,
,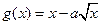 ,且
,且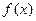 在
在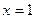 处取极值。
处取极值。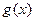 的单调性。
的单调性。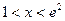 时,恒有
时,恒有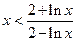 成立.
成立.
 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数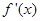 的最小值为
的最小值为 .
. ,
, ,
, 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数 的单调递增区间.
的单调递增区间. 上的最大值和最小值
上的最大值和最小值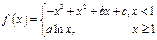 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 5.
5.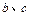 的值;
的值;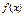 在区间
在区间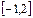 上的最大值;
上的最大值;