题目内容
已知圆C：（x-4）2+（y-3）2=1和两点 A（-m，0），B（m，0）（m＞0），若圆C上至少存在一点 P，使得∠APB=90°，则m的取值范围是．
考点：椭圆的简单性质
专题：平面向量及应用,直线与圆
分析：根据题意，得出圆C的圆心C与半径r，设点P（a，b）在圆C上，表示出
、
；
利用∠APB=90°，求出m2，根据|OP|表示的几何意义，得出m的取值范围．
| AP |
| BP |
利用∠APB=90°，求出m2，根据|OP|表示的几何意义，得出m的取值范围．
解答：
解：∵圆C：（x-4）2+（y-3）2=1，
∴圆心C（4，3），半径r=1；
设点P（a，b）在圆C上，则
=（a+m，b），
=（a-m，b）；
∵∠APB=90°，
∴
⊥
，
∴（a+m）（a-m）+b2=0；
即m2=a2+b2；
∴|OP|=
，
∴|OP|的最大值是|OC|+r=5+1=6，最小值是|OC|-r=5-1=4；
∴m的取值范围是[4，6]．
∴圆心C（4，3），半径r=1；
设点P（a，b）在圆C上，则
| AP |
| BP |
∵∠APB=90°，
∴
| AP |
| BP |
∴（a+m）（a-m）+b2=0；
即m2=a2+b2；
∴|OP|=
| a2+b2 |
∴|OP|的最大值是|OC|+r=5+1=6，最小值是|OC|-r=5-1=4；
∴m的取值范围是[4，6]．
点评：本题考查了平面向量的应用问题，也考查了直线与圆的应用问题，是综合性题目．
练习册系列答案
相关题目
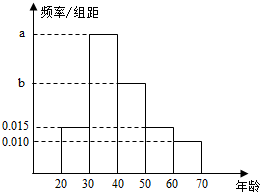根据某电子商务平台的调查统计显示，参与调查的1000位上网购物者的年龄情况如图显示．