题目内容
已知a，b都是正实数，且a+b=2，求证：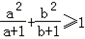
．
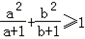．证明：因为a，b都是正实数，
所以原不等式等价于a2（b+1）+b2（a+1）≥（a+1）（b+1），
即 a2b+a2+ab2+b2≥ab+a+b+1．
等价于 a2+b2+ab（a+b）≥ab+a+b+1，
将a+b=2代入，只需要证明 a2+b2+ab=（a+b）2=4≥ab+3，
即ab≤1．而由已知 a+b=2≥2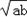
，可得ab≤1成立，所以原不等式成立．
所以原不等式等价于a2（b+1）+b2（a+1）≥（a+1）（b+1），
即 a2b+a2+ab2+b2≥ab+a+b+1．
等价于 a2+b2+ab（a+b）≥ab+a+b+1，
将a+b=2代入，只需要证明 a2+b2+ab=（a+b）2=4≥ab+3，
即ab≤1．而由已知 a+b=2≥2
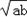，可得ab≤1成立，所以原不等式成立． 
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
已知a、b都是正实数，函数y=2aex+b的图象过（0，2）点，则
+
的最小值是（ ）
| 1 |
| a |
| 1 |
| b |
A、
| ||||
B、3+2
| ||||
| C、4 | ||||
| D、2 |
为矩阵
属于λ的一个特征向量，求实数a，λ的值及A2。
（α为参数），曲线D的参数方程为
，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。