题目内容
14.已知△ABC中,A=45°,a=2,b=$\sqrt{2}$,那么∠B为( )| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |
分析 根据正弦定理,求出sinB的值,再根据b<a得出B<A,即可求出B的值.
解答 解:△ABC中,A=45°,a=2,b=$\sqrt{2}$,
由正弦定理得,$\frac{a}{sinA}$=$\frac{b}{sinB}$,
∴sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{2}sin45°}{2}$=$\frac{1}{2}$;
又b<a,
∴B<A,
∴B=30°.
故选:A.
点评 本题考查了正弦定理的简单应用问题,是基础题目.

练习册系列答案
相关题目
19.某品牌新款夏装即将上市,为了对夏装进行合理定价,在该地区的三家连锁店各进行了两天试销售,得到如下数据:
(1)以三家连锁店分别的平均售价和平均销量为散点,求出售价与销量的回归直线方程$\widehaty=\widehatbx+\widehata$;
(2)在大量投入市场后,销售量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该款夏装在销售上获得最大利润,该款夏装的单价应定为多少元(保留整数)?$\left\{\begin{array}{l}\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})}({{y_i}-\overline y})}}{{{{\sum_{i=1}^n{({{x_i}-\overline x})}}^2}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline{xy}}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}\\ \widehata=\overline y-\widehatb\overline x\end{array}\right.$.
| 连锁店 | A店 | B店 | C店 | |||
| 售价x(元) | 80 | 86 | 82 | 88 | 84 | 90 |
| 销售量y(件) | 88 | 78 | 85 | 75 | 82 | 66 |
(2)在大量投入市场后,销售量与单价仍然服从(1)中的关系,且该夏装成本价为40元/件,为使该款夏装在销售上获得最大利润,该款夏装的单价应定为多少元(保留整数)?$\left\{\begin{array}{l}\widehatb=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})}({{y_i}-\overline y})}}{{{{\sum_{i=1}^n{({{x_i}-\overline x})}}^2}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline{xy}}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}\\ \widehata=\overline y-\widehatb\overline x\end{array}\right.$.
3.已知变量x,y之间的线性回归方程为$\widehat{y}$=-0.7x+10.3,且变量x,y之间的一组相关数据如表所示,则下列说法错误的是( )
| x | 6 | 8 | 10 | 12 |
| y | 6 | m | 3 | 2 |
| A. | 变量x,y之间呈现负相关关系 | |
| B. | m=4 | |
| C. | 可以预测,当x=11时,y=2.6 | |
| D. | 由表格数据知,该回归直线必过点(9,4) |
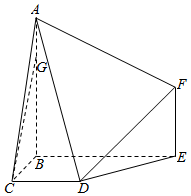 如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA,BC,BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.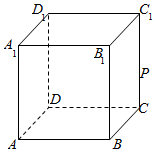 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.