题目内容
20.已函数f(x)=|x+1|+|x-3|.(1)作出函数y=f(x)的图象;
(2)若不等式f(x)≤ax的解集非空,求a的取值范围.
分析 (1)根据绝对值不等式的性质表示为分段函数形式进行作图即可.
(2)利用函数f(x)的图象,结合直线斜率的关系进行求解即可.
解答 解:(1)f(x)=|x+1|+|x-3|=$\left\{\begin{array}{l}{2x-2,}&{x≥3}\\{4,}&{-1<x<3}\\{-2x+2,}&{x≤-1}\end{array}\right.$,
则对应的图象为: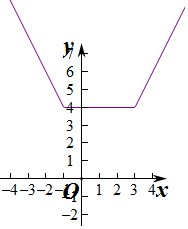
(2)当a=0时,y=0与f(x)的图象没有交点,此时不等式f(x)≤ax的解集为空集,不满足条件.
当a>0时,当直线y=ax经过点A(3,4)时,3a=4,即a=$\frac{4}{3}$,
要使不等式f(x)≤ax的解集非空,
则a≥$\frac{4}{3}$,
当a<0时,当直线y=ax的斜率a=-2时,f(x)与y=ax平行,没有交点,
要使使不等式f(x)≤ax的解集非空,则-2<a<0,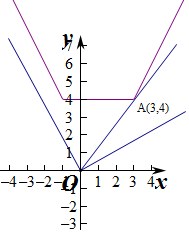
综上要使不等式f(x)≤ax的解集非空,则a≥$\frac{4}{3}$或-2<a<0.
点评 本题主要考查分段函数的应用,利用数形结合以及分类讨论的数学思想是解决本题的关键.考查学生的运算和推理能力.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
10.函数f(x)=x3-x+2在下列区间内一定存在零点的是( )
| A. | (1,2) | B. | (0,1) | C. | (-2,-1) | D. | (-1,0) |
8.若双曲线$\frac{x^2}{4}-\frac{y^2}{5}=1$与椭圆$\frac{x^2}{a^2}+\frac{y^2}{16}=1$有共同的焦点,且a>0,则a的值为( )
| A. | 5 | B. | $\sqrt{7}$ | C. | $\sqrt{15}$ | D. | $\sqrt{17}$ |