题目内容
5.已知数列{an},an=2an-1+3,a1=-1(1)设bn=an+3,求证:{bn}为等比数列;
(2)求{$\frac{1}{lo{g}_{2}{b}_{n}lo{g}_{2}{b}_{n+1}}$}的前n项和Sn.
分析 (1)n≥2,an=2an-1+3,a1=-1,变形为an+3=2(an-1+3),即bn=2bn-1,即可证明.
(2)由(1)可得:bn=2n.$\frac{1}{lo{g}_{2}{b}_{n}lo{g}_{2}{b}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.利用“裂项求和”方法即可得出.
解答 (1)证明:∵n≥2,an=2an-1+3,a1=-1,∴an+3=2(an-1+3),
∴bn=2bn-1,b1=2,
∴{bn}为等比数列,首项为2,公比为2.
(2)解:由(1)可得:bn=2n.
$\frac{1}{lo{g}_{2}{b}_{n}lo{g}_{2}{b}_{n+1}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
∴{$\frac{1}{lo{g}_{2}{b}_{n}lo{g}_{2}{b}_{n+1}}$}的前n项和Sn=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
点评 本题考查了等比数列的通项公式、“裂项求和”方法、对数运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.已知全集U=R,集合A={x|x2-2x-3>0},B={x|2<x<4},那么集合(∁UA)∩B=( )
| A. | {x|-1≤x≤4} | B. | {x|2<x≤3} | C. | {x|2≤x<3} | D. | {x|-1<x<4} |
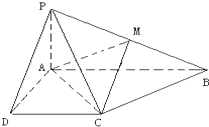 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.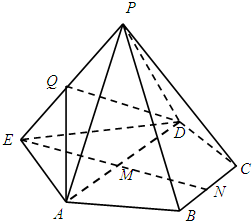 已知ABCD为等腰梯形,AD∥BC,AD=2,M,N分别为AD,BC的中点,MN=$\sqrt{3}$,现以AD为边,作两个正三角形△EAD与△PAD,如图,其中平面EAD与平面ABCD共面,平面PAD⊥平面ABCD,Q为PE
已知ABCD为等腰梯形,AD∥BC,AD=2,M,N分别为AD,BC的中点,MN=$\sqrt{3}$,现以AD为边,作两个正三角形△EAD与△PAD,如图,其中平面EAD与平面ABCD共面,平面PAD⊥平面ABCD,Q为PE