题目内容
17. 已知ABCD为等腰梯形,AD∥BC,AD=2,M,N分别为AD,BC的中点,MN=$\sqrt{3}$,现以AD为边,作两个正三角形△EAD与△PAD,如图,其中平面EAD与平面ABCD共面,平面PAD⊥平面ABCD,Q为PE
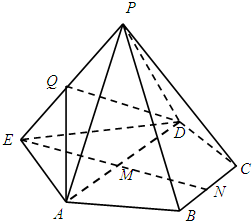
已知ABCD为等腰梯形,AD∥BC,AD=2,M,N分别为AD,BC的中点,MN=$\sqrt{3}$,现以AD为边,作两个正三角形△EAD与△PAD,如图,其中平面EAD与平面ABCD共面,平面PAD⊥平面ABCD,Q为PE的中点.
(Ⅰ)求证:平面QAD∥平面PBC;
(Ⅱ)求证:PE⊥平面PBC;
(Ⅲ)求AE与平面PDE所成角的正弦值.
分析 (I)连接QM,PN,由等腰梯形与等边三角形的性质可得:三点E,M,N共线.进而得出EM=MN,利用三角形中位线定理可得QM∥PN.QM∥平面PBC.同理可得AD∥平面PBC.即可证明平面QAD∥平面PBC.
(2)连接PM,△PAD是边长为2的等边三角形,AM=MD,可得PM=$\sqrt{3}$.可得EM=PM.又EQ=QP,可得PE⊥QM.同理利用等腰三角形的性质可得:EQ⊥AQ.可得PE⊥平面AQD,又平面QAD∥平面PBC,即可证明PE⊥平面PBC.
(3)PM⊥AD,平面PAD⊥平面ABCD,可得PM⊥平面ABCDE.PM⊥MN,AM⊥MN.建立如图所示的空间直角坐标系M-yxz.设平面EDP的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EP}=0}\\{\overrightarrow{n}•\overrightarrow{DP}=0}\end{array}\right.$,取$\overrightarrow{n}$.设AE与平面PDE所成角为θ,则sinθ=|cos$<\overrightarrow{n},\overrightarrow{AE}>$|=$\frac{|\overrightarrow{n}•\overrightarrow{AE}|}{|\overrightarrow{n}||\overrightarrow{AE}|}$,即可得出.
解答 (I)证明:连接QM,PN,由等腰梯形与等边三角形的性质可得:三点E,M,N共线.
∵△AED是边长为2的等边三角形,∴EM=$\sqrt{3}$,∴EM=MN.
又EQ=QP,∴QM∥PN.
∵QM?平面PBC,PN?平面PBC,
∴QM∥平面PBC.
由AD∥BC,同理可得AD∥平面PBC.
∵QM∩AD=M,QM,QD?平面QAD,
∴平面QAD∥平面PBC.
(2)证明:连接PM.
∵△PAD是边长为2的等边三角形,AM=MD,
∴PM=$\sqrt{3}$.
又EM=$\sqrt{3}$,∴EM=PM.
又EQ=QP,∴PE⊥QM.
又AP=AE,EQ=QP,∴EQ⊥AQ.
又AQ∩QM=Q,∴PE⊥平面AQD,
又平面QAD∥平面PBC,∴PE⊥平面PBC.
(3)解:∵PM⊥AD,平面PAD⊥平面ABCD,又平面PAD∩平面ABCD=AD,
∴PM⊥平面ABCDE.
∴PM⊥MN,又AM⊥MN.
建立如图所示的空间直角坐标系M-yxz.
则M(0,0,0),A(1,0,0),D(-1,0,0),E(0,-$\sqrt{3}$,0),P(0,0,$\sqrt{3}$).
∴$\overrightarrow{EP}$=(0,$\sqrt{3}$,$\sqrt{3}$),$\overrightarrow{DP}$=(1,0,$\sqrt{3}$),$\overrightarrow{AE}$=(-1,-$\sqrt{3}$,0).
设平面EDP的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EP}=0}\\{\overrightarrow{n}•\overrightarrow{DP}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{\sqrt{3}y+\sqrt{3}z=0}\\{x+\sqrt{3}z=0}\end{array}\right.$,取$\overrightarrow{n}$=($\sqrt{3}$,1,-1).
设AE与平面PDE所成角为θ,则sinθ=|cos$<\overrightarrow{n},\overrightarrow{AE}>$|=$\frac{|\overrightarrow{n}•\overrightarrow{AE}|}{|\overrightarrow{n}||\overrightarrow{AE}|}$=$\frac{2\sqrt{3}}{2×\sqrt{5}}$=$\frac{\sqrt{15}}{5}$.
∴AE与平面PDE所成角的正弦值为$\frac{\sqrt{15}}{5}$.
点评 本题考查了线面平面平行的判定与性质定理、线面面面垂直的判定与性质定理、法向量的应用、向量夹角公式,考查了推理能力与计算能力,属于中档题.

| A. | 0 | B. | 1 | C. | 2 | D. | -3 |
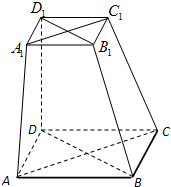 如图,在六面体中ABCD-A1B1C1D1,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.
如图,在六面体中ABCD-A1B1C1D1,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.