题目内容
【题目】如图,在三棱锥![]() 中,底面是边长为4的正三角形,
中,底面是边长为4的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
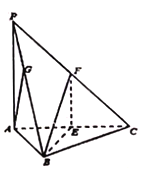
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)见解析(2)见解析
【解析】
(1)先证明![]() ,
,![]() ,可得
,可得![]() 平面
平面![]() 从而平面
从而平面![]() 平面
平面![]() ;
;
(2)由题意可知![]() 两两垂直,分别以
两两垂直,分别以![]() 方向为
方向为![]() 轴建立坐标系,求出平面
轴建立坐标系,求出平面![]() 的法向量及
的法向量及![]() ,代入公式可得未知量的方程,解之即可.
,代入公式可得未知量的方程,解之即可.
(1)证明:∵![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]()
∵![]()
∴![]() 平面
平面![]()
∵![]() 平面
平面![]()
∴平面![]() 平面
平面![]()
(2)解:如图,由(1)知,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() ,∴
,∴![]() ,
,![]() ,又
,又![]() ,
,
∴![]() 两两垂直,分别以
两两垂直,分别以![]() 方向为
方向为![]() 轴建立坐标系.
轴建立坐标系.

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]()
所以![]()
![]() ,
,![]() ,设平面
,设平面![]() 的法向量
的法向量![]() ,则
,则
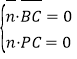 ,
,![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
∴![]()
由已知![]()
![]()
![]() 或
或![]() (舍去)
(舍去)
故![]()
故线段![]() 上存在点
上存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,
,
此时![]() 为线段
为线段![]() 的中点.
的中点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球,根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:
奖级 | 摸出红、蓝球个数 | 获奖金额 |
一等奖 | 3红1蓝 | 200元 |
二等奖 | 3红0蓝 | 50元 |
三等奖 | 2红1蓝 | 10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级.
(1)求摸奖者第一次摸球时恰好摸到1个红球的概率;
(2)求摸奖者在一次摸奖中获奖金额![]() 的分布列.
的分布列.