题目内容
设关于 不等式
不等式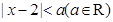 的解集为
的解集为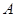 ,且
,且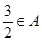 ,
,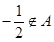 .
.
(1)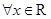 ,
,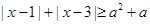 恒成立,且
恒成立,且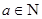 ,求
,求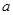 的值;
的值;
(2)若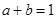 ,求
,求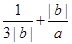 的最小值并指出取得最小值时
的最小值并指出取得最小值时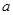 的值.
的值.
(1) ;(2)最小值是
;(2)最小值是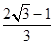 ,取最小值时
,取最小值时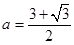 .
.
解析试题分析:(1)由于关于 不等式
不等式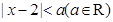 的解集为
的解集为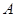 ,且
,且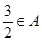 ,
,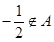 .得出
.得出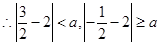 ,解得
,解得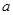 的范围;又
的范围;又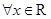 ,
,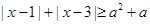 恒成立,即
恒成立,即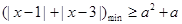 ,即
,即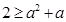 ,再根据
,再根据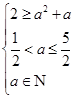 求得实数
求得实数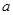 的值;(2)根据
的值;(2)根据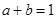 ,把
,把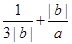 变形为
变形为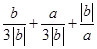 用均值不等式求解.注意等号成立的条件.
用均值不等式求解.注意等号成立的条件.
试题解析:(1)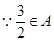 ,
,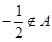
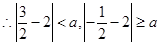 ,
,
即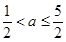 2分
2分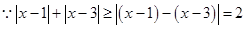

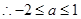 ,
,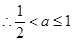
又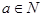
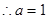 6分
6分
(2)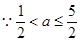
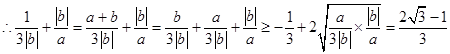 9分
9分
当且仅当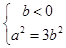 ,即
,即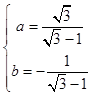 时上式取等号
时上式取等号
又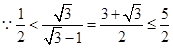
所以,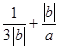 的最小值是
的最小值是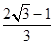 ,取最小值时
,取最小值时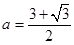 12分
12分
考点:绝对值不等式,均值不等式,恒成立.

练习册系列答案
相关题目
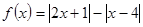 .
.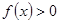 ;
; 对一切实数
对一切实数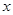 均成立,求
均成立,求 的取值范围.
的取值范围.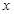 的不等式
的不等式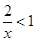 .
.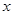 的不等式
的不等式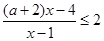 (其中
(其中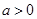 ).
).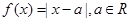
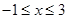 时,
时,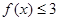 ,求a的取值范围;
,求a的取值范围;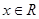 ,
,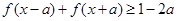 恒成立,求实数a的最小值
恒成立,求实数a的最小值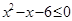 解集为
解集为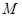 ,不等式
,不等式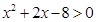 解集为
解集为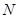 ,不等式
,不等式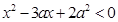
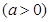 解集为
解集为 .
.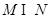 ;
; 的取值范围.
的取值范围.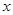 的不等式
的不等式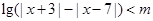 .
.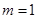 时,解此不等式;
时,解此不等式;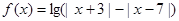 ,当
,当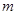 为何值时,
为何值时,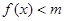 恒成立?
恒成立?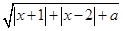 .
.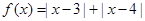 .
. ;
; ,
,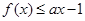 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.