题目内容
设函数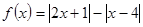 .
.
(1)解不等式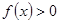 ;
;
(2)若 对一切实数
对一切实数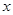 均成立,求
均成立,求 的取值范围.
的取值范围.
(1)  ;(2)
;(2) 
解析试题分析:(1) 不等式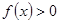 即
即 是含两个绝对值符号的不等式,用零点分段讨论法解;(2)由
是含两个绝对值符号的不等式,用零点分段讨论法解;(2)由  对一切实数
对一切实数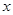 均成立
均成立 对一切实数
对一切实数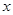 均成立,令
均成立,令 ,则
,则 ,应用三角不等式可求得
,应用三角不等式可求得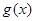 的最小值,从而问题获得解决.
的最小值,从而问题获得解决.
试题解析:(1)当 时,由
时,由 ,得
,得 ,所以
,所以 ;
;
当 时,由
时,由 ,得
,得 ,所以
,所以 ; 当
; 当 时,由
时,由 ,得
,得 ,所以
,所以 ;
;
综上,不等式的解集为
(2) 由  对一切实数
对一切实数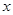 均成立
均成立 对一切实数
对一切实数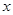 均成立,令
均成立,令 ,因为
,因为 所以
所以 ,故知
,故知
考点:1.绝对值不等式;2.不等式的恒成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的解集为
的解集为 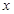 的不等式
的不等式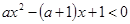
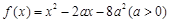 ,记不等式
,记不等式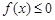 的解集为
的解集为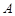 .
.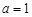 时,求集合
时,求集合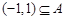 ,求实数
,求实数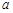 的取值范围.
的取值范围.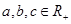 ,且
,且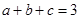 ,
,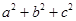 的最小值为
的最小值为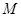 .
.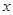 的不等式
的不等式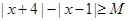 .
.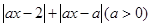 .
. 不等式
不等式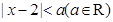 的解集为
的解集为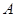 ,且
,且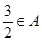 ,
,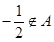 .
.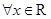 ,
,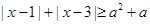 恒成立,且
恒成立,且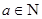 ,求
,求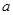 的值;
的值;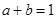 ,求
,求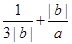 的最小值并指出取得最小值时
的最小值并指出取得最小值时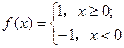 ,则不等式
,则不等式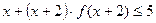 的解集是__________
的解集是__________