题目内容
关于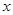 的不等式
的不等式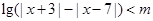 .
.
(Ⅰ)当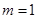 时,解此不等式;
时,解此不等式;
(Ⅱ)设函数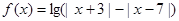 ,当
,当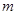 为何值时,
为何值时,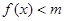 恒成立?
恒成立?
(1)解集为 ;(2)
;(2) .
.
解析试题分析:本题考查绝对值不等式的解法和不等式的恒成立问题,考查学生的分类讨论思想和转化能力.第一问,先将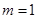 代入,利用对数值得
代入,利用对数值得 ,利用零点分段法去绝对值解不等式;第二问,先将已知转化为
,利用零点分段法去绝对值解不等式;第二问,先将已知转化为 ,利用绝对值的几何意义得到
,利用绝对值的几何意义得到 的最大值,所以
的最大值,所以 ,即
,即 .
.
试题解析:(1)当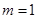 时,原不等式可变为
时,原不等式可变为 ,
,
可得其解集为
(2)设 ,
,
则由对数定义及绝对值的几何意义知 ,
,
因 在
在 上为增函数,
上为增函数,
则 ,当
,当 时,
时, ,
,
故只需 即可,
即可,
即 时,
时,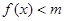 恒成立.
恒成立.
考点:1.解绝对值不等式;2.绝对值的几何意义;3.函数的最大值.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
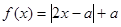 .
.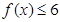 的解集为
的解集为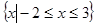 ,求实数a的值;(5分)
,求实数a的值;(5分)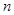 使
使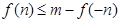 成立,求实数
成立,求实数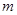 的取值范围.(5分)
的取值范围.(5分) 不等式
不等式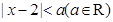 的解集为
的解集为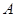 ,且
,且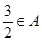 ,
,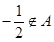 .
.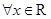 ,
,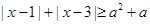 恒成立,且
恒成立,且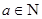 ,求
,求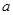 的值;
的值;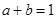 ,求
,求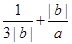 的最小值并指出取得最小值时
的最小值并指出取得最小值时 若
若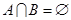 ,求实数
,求实数 的取值范围;
的取值范围;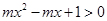 ,对任意实数
,对任意实数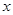 都成立,求
都成立,求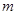 的取值范围.
的取值范围.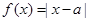 .
.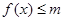 的解集为
的解集为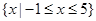 ,求实数
,求实数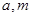 的值.
的值.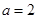 且
且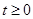 时,解关于
时,解关于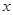 的不等式
的不等式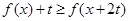 .
.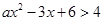 的解集为
的解集为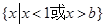 .
.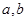 的值;
的值; 不等式:
不等式: .
.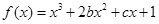 的两个极值点为
的两个极值点为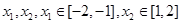 ,求
,求 的取值范围。
的取值范围。