题目内容
已知A,B两点分别在直线y=
与y=-
上,且|AB|=2
,又点P为AB的中点.
(1)求点P的轨迹方程.
(2)若不同三点D(-2,0),S,T均在P的轨迹上,且
•
=0,求T点横坐标xT的取值范围.
| x | ||
|
| x | ||
|
| 2 |
(1)求点P的轨迹方程.
(2)若不同三点D(-2,0),S,T均在P的轨迹上,且
| DS |
| ST |
分析:(1)设出A,B的坐标,利用点P为AB的中点,确定坐标之间的关系,根据|AB|=2
,建立方程,化简,即可求点P的轨迹方程.
(2)直线DS、ST分别代入椭圆方程,求出T点横坐标,利用基本不等式,即可求T点横坐标xT的取值范围.
| 2 |
(2)直线DS、ST分别代入椭圆方程,求出T点横坐标,利用基本不等式,即可求T点横坐标xT的取值范围.
解答:解:(1)设A(m,
),B(n,-
),则|AB|=
=2
.
设P(x,y),则
,∴
=2
,
化简可得y2+
=1;
(2)设S(x1,y1),直线DS为y=k(x+2),代入椭圆方程,整理可得(1+4k2)x2+16k2x+4k2-1=0,则xD+x1=
∴x1=
,y1=
,
则直线ST为y=-
(x-x1)+y1,化简为y=-
+
,
代入椭圆方程可得(1+
)x2+
x+
-4=0,
∴x1+xT=
,
∴xT=
-
=2-
(因为三点不同,易知k≠0)=2-
=
≥2-
=
∴xT的取值范围为[
,+∞).
| m | ||
|
| n | ||
|
(m-n)2+
|
| 2 |
设P(x,y),则
|
(2
|
| 2 |
化简可得y2+
| x2 |
| 4 |
(2)设S(x1,y1),直线DS为y=k(x+2),代入椭圆方程,整理可得(1+4k2)x2+16k2x+4k2-1=0,则xD+x1=
| -16k2 |
| 1+4k2 |
∴x1=
| 2-8k2 |
| 1+4k2 |
| 4k |
| 1+4k2 |
则直线ST为y=-
| 1 |
| k |
| x |
| k |
| 2-4k2 |
| 4k(1+4k2) |
代入椭圆方程可得(1+
| 4 |
| k2 |
| 32k2-16 |
| k2(1+4k2) |
| 4(2-4k2)2 |
| k2(1+4k2)2 |
∴x1+xT=
| 16-32k2 |
| (4+k2)(1+4k2) |
∴xT=
| 16-32k2 |
| (4+k2)(1+4k2) |
| 2-8k2 |
| 1+4k2 |
| 36k2 |
| 4k4+17k2+4 |
| 36k2 |
| 4k4+17k2+4 |
| 36 | ||
4(k2+
|
| 36 |
| 25 |
| 14 |
| 25 |
∴xT的取值范围为[
| 14 |
| 25 |
点评:本题考查轨迹方程,考查代入法的运用,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
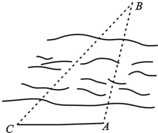 如图,已知A,B两点分别在河的两岸,某测量者在点A所在的河岸边另选定一点C,测得AC=50m,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )
如图,已知A,B两点分别在河的两岸,某测量者在点A所在的河岸边另选定一点C,测得AC=50m,∠ACB=45°,∠CAB=105°,则A、B两点的距离为( )A、50
| ||
B、25
| ||
C、25
| ||
D、50
|
 ,则线段AB的长为( )
,则线段AB的长为( )