Question

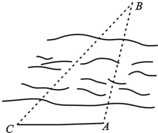如图，已知A，B两点分别在河的两岸，某测量者在点A所在的河岸边另选定一点C，测得AC=50m，∠ACB=45°，∠CAB=105°，则A、B两点的距离为（　　）

• A、50

  3

  m
• B、25

  3

  m
• C、25

  2

  m
• D、50

  2

  m

Answer 1

分析：依题意在A，B，C三点构成的三角形中利用正弦定理，根据AC，∠ACB，B的值求得AB

解答：解：由正弦定理得

AB

sin∠ACB

=

AC

sin∠B

，
∴AB=

AC•sin∠ACB

sin∠B

=

50• 2 2

1 2

=50

2

，
∴A，B两点的距离为50

2

m，
故选：D．

点评：本题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．