题目内容
4.甲、乙两楼相距20m,从乙楼底望甲楼顶的仰角为60°,从甲楼顶望乙楼顶的俯角为30°,则甲楼高和乙楼高的比为3:2.分析 由题意画出图形,过点C作CM⊥AB于点M,根据题意得:CM=BD=20米,∠ACM=30°,∠ADB=60°,然后在Rt△ACM与Rt△ADB中,用正切函数计算求得两楼的高度,即可得出结论.
解答 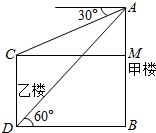 解:如图过点C作CM⊥AB于点M,根据题意得:CM=BD=20米,
解:如图过点C作CM⊥AB于点M,根据题意得:CM=BD=20米,
∠ACM=30°,∠ADB=60°,
在Rt△ACM中,tan30°=$\frac{AM}{CM}$=$\frac{\sqrt{3}}{3}$
∴AM=$\frac{\sqrt{3}}{3}$CM=20×$\frac{\sqrt{3}}{3}$=$\frac{20\sqrt{3}}{3}$(米),
在Rt△ADB中,tan60°=$\frac{AB}{BD}$
∴AB=DB•tan60°=20$\sqrt{3}$(米),
CD=AB-AM=20$\sqrt{3}$-$\frac{20\sqrt{3}}{3}$=$\frac{40\sqrt{3}}{3}$(米)
所以甲楼高和乙楼高的比为3:2,
故答案为3:2.
点评 本题考查了应用正弦定理、余弦定理解三角形应用题问题;一般是根据题意,从实际问题中抽象出一个或几个三角形,通过解这些三角形,从而使实际问题得到解决.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
3.集合A={x|x>0},B={-2,-1,1,2},则(∁RA)∩B=( )
| A. | (0,+∞) | B. | {-2,-1,1,2} | C. | {-2,-1} | D. | {1,2} |
9.已知集合M={y|y=x2},用自然语言描述M应为( )
| A. | 函数y=x2的函数值组成的集合 | B. | 函数y=x2的自变量的值组成的集合 | ||
| C. | 函数y=x2的图象上的点组成的集合 | D. | 以上说法都不对 |
16.在平行四边形ABCD中,∠BAD=60°,E是CD上一点,且$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\overrightarrow{BC}$,|$\overrightarrow{AB}$|=λ|$\overrightarrow{AD}$|.若$\overrightarrow{AC}$•$\overrightarrow{EB}$=$\frac{1}{2}$$\overrightarrow{AD}$2,则λ等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
13.从某地区一次中学生知识竞赛中,随机抽取了30名学生的成绩,绘成如图所示的2×2列联表:
(1)试问有没有90%的把握认为优秀一般与性别有关;
(2)用样本估计总体,把频率作为概率,若从该地区所有的中学(人数很多)中随机抽取3人,用ξ表示所选3人中优秀的人数,试写出ξ的分布列,并求出ξ的数学期望,.${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$,其中n=a+b+c+d
独立性检验临界表:
| 优秀 | 一般 | 合计 | |
| 男生 | 7 | 6 | |
| 女生 | 5 | 12 | |
| 合计 |
(2)用样本估计总体,把频率作为概率,若从该地区所有的中学(人数很多)中随机抽取3人,用ξ表示所选3人中优秀的人数,试写出ξ的分布列,并求出ξ的数学期望,.${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({a+d})({a+c})({b+d})}}$,其中n=a+b+c+d
独立性检验临界表:
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
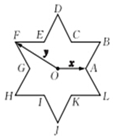 将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5.
将圆的六个等分点分成相同的两组,它们每组三个点构成的两个正三角形除去内部的六条线段后可以形成一个正六角星.如图所示的正六角星的中心为点O,其中x,y分别为点O到两个顶点的向量.若将点O到正六角星12个顶点的向量都写成ax+by的形式,则a+b的最大值为5.