题目内容
函数 在
在 上是增函数,
上是增函数, 若
若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B.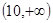 |
C. | D.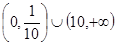 |
C
解析试题分析:∵ 且
且 ,∴
,∴ ,又函数
,又函数 在
在 上是增函数,∴
上是增函数,∴ ,∴
,∴ ,∴
,∴ ,即
,即 的取值范围是
的取值范围是
考点:本题考查了函数性质的运用
点评:对于抽象函数不等式的解法往往利用单调性转化为常见不等式的解法

练习册系列答案
相关题目
函数 在区间
在区间 上递减,则实数
上递减,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数 ,且关于x的方程
,且关于x的方程 有6个不同的实数解,若最小实数解为
有6个不同的实数解,若最小实数解为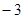 ,则
,则 的值为( )
的值为( )
| A.-3 | B.-2 | C.0 | D.不能确定 |
函数 +1(a>0,a≠1)的图象必经过定点 ( )
+1(a>0,a≠1)的图象必经过定点 ( )
| A.(0,1) | B.(2,1) | C.(2,2) | D.(2,3) |
设 是定义在R上的函数且
是定义在R上的函数且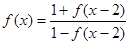 ,且
,且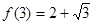 ,则
,则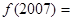
A.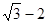 | B.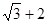 | C. | D.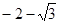 |
下列函数是偶函数,且在 上单调递减的是 ( )
上单调递减的是 ( )
A. | B. | C. | D. |
下列函数在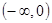 上是增函数的是( )
上是增函数的是( )
A.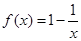 | B.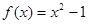 | C. | D.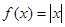 |
 的长为x,f(x)表示孤
的长为x,f(x)表示孤

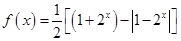 的图象大致为 ( )
的图象大致为 ( )