题目内容
已知函数 ,且关于x的方程
,且关于x的方程 有6个不同的实数解,若最小实数解为
有6个不同的实数解,若最小实数解为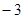 ,则
,则 的值为( )
的值为( )
| A.-3 | B.-2 | C.0 | D.不能确定 |
B
解析试题分析:作出函数 的图象,因为方程
的图象,因为方程 有6个不同的实数解,所以如图所示:令t=f(x),方程
有6个不同的实数解,所以如图所示:令t=f(x),方程 转化为:t2+at+2b=0,则方程有一零根和一正根,又因为最小的实数解为-3,所以f(-3)=2,所以方程:t2+at+2b=0的两根是0和2,,由韦达定理得:a=-2,b=0,∴a+b=-2,故选B。
转化为:t2+at+2b=0,则方程有一零根和一正根,又因为最小的实数解为-3,所以f(-3)=2,所以方程:t2+at+2b=0的两根是0和2,,由韦达定理得:a=-2,b=0,∴a+b=-2,故选B。
考点:根的存在性及方程解的个数的判断;函数图像的对称变换。
点评:本题主要考查函数与方程的综合运用,还考查了方程的根与函数零点的关系,属于中档题.做本题的关键是正确、快速画出函数 的图像,以及把方程
的图像,以及把方程 的解和方程t2+at+2b=0的解联系起来。
的解和方程t2+at+2b=0的解联系起来。

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
若函数 与函数
与函数 在区间
在区间 上都是减函数,则实数的取值范围为( )
上都是减函数,则实数的取值范围为( )
A. | B. | C. | D.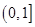 |
下列函数中,满足 的是( )
的是( )
A. | B.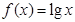 | C. | D. |
设 ,用二分法求方程
,用二分法求方程 内近似解的过程中得
内近似解的过程中得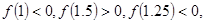 则方程的根落在区间( )
则方程的根落在区间( )
A. | B. | C. | D.不能确定 |
已知 ,
, ,则有:( )
,则有:( )
A. | B. |
C. | D.以上都不是 |
函数 在
在 上是增函数,
上是增函数, 若
若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B.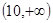 |
C. | D.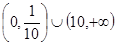 |
函数 的定义域为开区间
的定义域为开区间 ,导函数
,导函数 在
在 内的图象如图所示,则函数
内的图象如图所示,则函数 在开区间
在开区间 内有极小值点( )
内有极小值点( )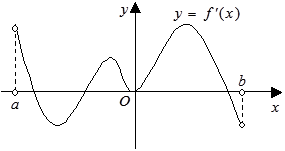
| A.4个 | B. 个 个 | C. 个 个 | D.1个 |
 时,在同一坐标系中,函数
时,在同一坐标系中,函数 与
与 的图象是
的图象是
 的图象的是
的图象的是