题目内容

5．在△ABC中，高AD把BC分为长2cm和3cm的两段，∠A=45°，则S△ABC=15．

分析 作出图象，由正切函数定义和两角和的正切可得三角形的高，由面积公式可得．

解答 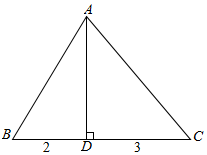解：如图设AD=h，则在RT△ABD中，tan∠BAD=$\frac{2}{h}$，
同理在RT△ACD中，tan∠CAD=$\frac{3}{h}$，
故tan∠BAC=tan（∠BAD+∠CAD）=$\frac{\frac{2}{h}+\frac{3}{h}}{1-\frac{2}{h}•\frac{3}{h}}$=tan45°=1，
解关于h的方程舍去负根可得h=6，
故S△ABC=$\frac{1}{2}$×5×6=15，
故答案为：15．

点评 本题考查三角形的面积，数形结合并利用和差角的三角函数是解决问题的关键，属中档题．

练习册系列答案
相关题目
15．已知各项都为正数的等比数列{an}，公比q=2，若存在两项am，an，使得$\sqrt{{a}_{m}{a}_{n}}$=2a1，则$\frac{1}{n}+\frac{4}{m}$的最小值为$\frac{7}{3}$．
16．已知数列{an}的前n的项和为Sn，an≠0，且2Sn是a1与anan+1的等差中项．
（1）若a1=1，求数列{an}的通项公式；
（2）在（1）的条件下，求数列{$\frac{（-1）^{n}•n}{{{a}_{n}a}_{n+1}}$}的前n项和Tn．
13．设数列{an}，（n≥1，n∈N）满足a1=2，a2=6，且（an+2-an+1）-（an+1-an）=2，若[x]表示不超过x的最大整数，则[$\frac{2016}{{a}_{1}}$+$\frac{2016}{{a}_{2}}$+…+$\frac{2016}{{a}_{2016}}$]=2015．
20．若函数y=cosx的值域是[0，1]，则x的取值范围是[2kπ-$\frac{π}{2}$，2kπ+$\frac{π}{2}$]，k∈Z．
1．已知点P1（a1，b1），P2（a2，b2），…Pn（an，bn），（n为正整数）都在函数y=（$\frac{1}{2}$）x的图象上．
（1）若数列{an}是等差数列，证明：数列{bn}是等比数列；
（2）设an=n，（n∈N+），过点Pn，Pn+1的直线与两坐标轴所围成的三角形面积为cn，试求最小的实数t，使cn≤t对一切正整数n恒成立；
（3）对（2）中的数列{an}，对每个正整数k，在ak与ak+1之间插入3k-1个3，得到一个新的数列{dn}，设Sn是数列{dn}的前n项和，试探究2016是否是数列{Sn}中的某一项，写出你探究得到的结论并给出证明．
8．设双曲线C：$\frac{y^2}{4}$-x2=1，则其两焦点的坐标为（0，±$\sqrt{5}$）；若双曲线C1经过点（$\sqrt{5}$，-2），且与双曲线C具有相同的渐近线，则双曲线C1的方程为x2-$\frac{{y}^{2}}{4}$=1．
5．已知函数f（x）=2x-3x2，设数列{an}满足：a1=$\frac{1}{4}$，an+1=f（an）
（1）求证：对任意的n∈N*，都有0＜an＜$\frac{1}{3}$；
（2）求证：$\frac{3}{1-3{a}_{1}}$+$\frac{3}{1-3{a}_{2}}$+…+$\frac{3}{1-3{a}_{n}}$≥4n+1-4．
6．已知函数f（x）=$\left\{\begin{array}{l}sin（x+α），x≤0\\ cos（x+α），x＞0\end{array}$，则“α=$\frac{π}{4}$”是“函数f（x）是偶函数“的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网