题目内容
2sin130°+sin100°(1+
| ||
|
分析：分子把130°=180°-50°，100°=180°-80°，370°=360°+10°利用诱导公式分别化简，再根据同角三角函数间的基本关系及特殊角的三角函数值，和差化积公式进行化简，分母利用二倍角的余弦公式化简，约分可得值．
解答：解：原式=
=
=
=
=
=
=
=
=
=2
故答案为2．
2sin50°+sin80°(1+
| ||
|
2sin50°+cos10°(1+
| ||||
|
=
2sin50°+cos10°+
| ||
|
2sin50°+2(
| ||||||
|
| 2sin50°+2sin(10°+30°) | ||
|
| 2(sin50°+sin40°) | ||
|
=
| 4sin45°cos5° | ||
|
| 4sin45° | ||
|
2
| ||
|
故答案为2．
点评：此题为一道中档题，要求学生灵活变换角度运用诱导公式进行化简求值，以及灵活运用同角三角函数间的基本关系及和差化积公式、特殊角的三角函数值进行化简求值．此题的难点是角度的变换．
练习册系列答案
提分百分百检测卷系列答案
相关题目
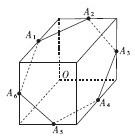如图，圆O过正方体六条棱的中点Ai（i=1，2，3，4，5，6），此圆被正方体六条棱的中点分成六段弧，记弧AiAi+1在圆O中所对的圆心角为αi（i=1，2，3，4，5），弧A6A1所对的圆心角为α6，则sin| α1 |
| 4 |
| α3+α5 |
| 4 |
| α2 |
| 4 |
| α4+α6 |
| 4 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
若b＞a＞0，满足tanα=
，且sinα=
的角α的集合是（ ）
| a2-b2 |
| 2ab |
| b2-a2 |
| a2+b2 |
A、{α|0＜α＜
| ||
B、{α|
| ||
| C、{α|2kπ≤α≤π+2kπ，k∈Z} | ||
D、{α|
|
若sinα=m，α为第二象限角，则tan2α的值为（ ）
A、-
| ||||
B、
| ||||
C、±
| ||||
| D、以上全不对 |