题目内容
9.在平面四边形ABCD中,若AB=1,BC=2,B=60°,C=45°,D=120°,则AD=$\frac{\sqrt{6}-\sqrt{2}}{2}$.分析 在△ABC中,由余弦定理可得AC,求出∠ACD=15°,在△ACD中,∠D=120°,由正弦定理可得AD.
解答 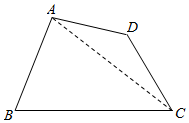 解:连接AC,在△ABC中,由余弦定理可得AC=$\sqrt{1+4-2×1×2×cos60°}$=$\sqrt{3}$,
解:连接AC,在△ABC中,由余弦定理可得AC=$\sqrt{1+4-2×1×2×cos60°}$=$\sqrt{3}$,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∴∠ACB=30°,
∴∠ACD=15°.
在△ACD中,∠D=120°,由正弦定理可得AD=$\frac{\sqrt{3}sin15°}{sin120°}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{6}-\sqrt{2}}{2}$.
点评 本题考查余弦定理、正弦定理的运用,考查学生的计算能力,求出AC,∠ACD是关键.

练习册系列答案
相关题目
20.已知集合M={y|y=2sinx,x∈R},N={x|y=lgx},则M∩N为( )
| A. | [-2,2] | B. | (0,+∞) | C. | (0,2] | D. | [0,2] |
17.已知等差数列{an}的前n项和为Sn,a1=-7,S8=0.
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足b1=$\frac{1}{16}$,bnbn+1=2an,求数列{bn}的通项公式.
(Ⅰ)求{an}的通项公式;
(Ⅱ)数列{bn}满足b1=$\frac{1}{16}$,bnbn+1=2an,求数列{bn}的通项公式.
4.已知定义在R上的偶函数f(x),满足f(x+4)=f(x),f(x)=sinπx+2|sinπx|,x∈[0,2],函数g(x)=f(x)-loga(x+$\frac{3}{2}$),若以g(x)=0在区间[-1,3]上至少6个根,则a的取值范围为( )
| A. | [${4}^{\frac{1}{3}}$,+∞) | B. | [${4}^{\frac{1}{3}}$,6] | C. | [4,+∞) | D. | [3,4] |
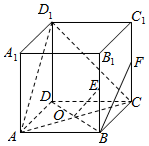 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱BB1、CC1的中点,AC与BD交于点O.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别是棱BB1、CC1的中点,AC与BD交于点O.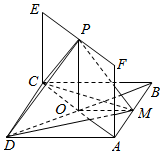 如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在的平面,BD与AC的交点为O,M,P分别为AB,EF的中点,AB=2,AF=1.
如图所示,已知正方形ABCD所在平面垂直于矩形ACEF所在的平面,BD与AC的交点为O,M,P分别为AB,EF的中点,AB=2,AF=1. (重点中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).质点走完的第99段与第1段所在的直线所成的角是( )
(重点中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).质点走完的第99段与第1段所在的直线所成的角是( )