题目内容
6．函数y=$\frac{x{a}^{x}}{|x|}$（0＜a＜1）的图象的大致形状是④（填正确的序号）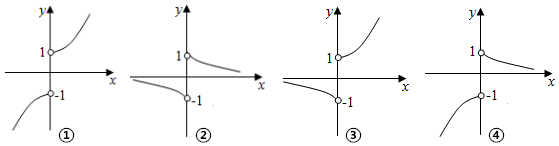
分析 化简函数解析式，利用指数函数的性质判断函数的单调性即可得出答案．
解答 解：y=$\left\{\begin{array}{l}{{a}^{x}，x＞0}\\{-{a}^{x}，x＜0}\end{array}\right.$，
∵0＜a＜1，
∴y=ax是减函数，y=-ax是增函数，
∴y=$\frac{x{a}^{x}}{|x|}$在（0，+∞）上单调递减，在（-∞，0）上单调递增，
故答案为④．
点评 本题考查了指数函数的图象与性质，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
16．“a≥3${∫}_{0}^{\frac{π}{6}}$cosθdθ”是“直线l：2ax-y+2a2=0（a＞0）与双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4}$=1的右支无交点”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
17．过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左焦点F（-c，0）（c＞0），作圆x2+y2=a2的切线，切点为E，延长FE交双曲线右支于点P，若$\overrightarrow{OE}=\frac{1}{2}（{\overrightarrow{OF}+\overrightarrow{OP}}）$，则双曲线的离心率为（ ）
| A． | $2\sqrt{5}$ | B． | $\sqrt{5}$ | C． | $\frac{{\sqrt{10}}}{2}$ | D． | $\frac{{\sqrt{10}}}{5}$ |
14．设向量$\overrightarrow{AB}=（1，4），\overrightarrow{BC}=（m，-1）$，且$\overrightarrow{AB}⊥\overrightarrow{BC}$，则实数m的值为（ ）
| A． | -10 | B． | -13 | C． | -7 | D． | 4 |