题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若对![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(1)![]() (2)
(2)![]() (3)
(3) ![]()
【解析】试题分析:(1)将a=1代入求出函数的表达式,通过求导令导函数大于0,从而求出函数的单调递增区间;(2)问题转化为![]() 对1≤x≤e恒成立.记h(x)=
对1≤x≤e恒成立.记h(x)=![]() ,通过求导得到h(x)的单调性,从而求出a的范围;(3)先求出函数的导数,通过讨论当0<x<ln2k时,当ln2k<x<k时的情况,从而得到函数f(x)的最大值.
,通过求导得到h(x)的单调性,从而求出a的范围;(3)先求出函数的导数,通过讨论当0<x<ln2k时,当ln2k<x<k时的情况,从而得到函数f(x)的最大值.
试题解析:
⑴![]() 时,
时, ![]() ,
, ![]() ,令
,令![]() ,得
,得![]() ,解得
,解得![]() .
.
所以函数![]() 的单调增区间为
的单调增区间为![]() .
.
⑵由题意 ![]() 对
对![]() 恒成立,因为
恒成立,因为![]() 时,
时, ![]() , 所以
, 所以![]() 对
对![]() 恒成立.记
恒成立.记![]() ,因为
,因为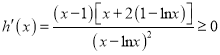 对
对![]() 恒成立,当且仅当
恒成立,当且仅当![]() 时
时![]() ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,因此
,因此![]() .
.
⑶ 因为![]() ,由
,由![]() ,得
,得![]() 或
或![]() (舍).
(舍).
可证![]() 对任意
对任意![]() 恒成立,所以
恒成立,所以![]() ,
,
因为![]() ,所以
,所以![]() ,由于等号不能同时成立,所以
,由于等号不能同时成立,所以![]() ,于是
,于是![]() .
.
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调减函数;
上是单调减函数;
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调增函数.
上是单调增函数.
所以![]() ,
,
记![]() ,
, ![]() ,以下证明当
,以下证明当![]() 时,
时, ![]() .
.
![]() ,记
,记![]() ,
, ![]() 对
对![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调减函数,
上单调减函数, ![]() ,
, ![]() ,所以
,所以![]() ,使
,使![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调增函数;当
上是单调增函数;当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是单调减函数.又
上是单调减函数.又![]() ,所以
,所以![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,所以
恒成立,所以![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目