Question

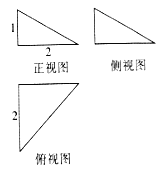
【题目】如图是某几何体的三视图.

（1）求该几何体外接球的体积；

（2）求该几何体内切球的半径.

Answer 1

【答案】(1) ；(2) .

【解析】试题分析：（1）由三视图可知，几何体是三条侧棱两两垂直的三棱锥，以三条两两垂直的侧棱的长构造一个长方体，则该长方体的对角线长等于其外接球的直径，算出半径的长。（2）设内切球的半径为，球心为，连接，把三棱锥分成四个小三棱锥，由这四个小三棱锥的体积和等于三棱锥的体积，求出内切球的半径。

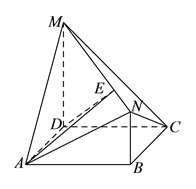
试题解析：（1）由三视图可知，几何体是三条侧棱两两垂直的三棱锥，如图，设为三棱锥.

以为长、宽、高构造一个长方体，则该长方体的对角线长等于其外接球的直径，

设该外接球半径为.

∴，∴.

∴外接球的体积为.

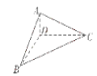
（2）设内切球的半径为，球心为，连接，把三棱锥分成四个小三棱锥，四个小三棱锥的体积和等于三棱锥的体积.

∴ .

解得.

∴所求几何体内切球的半径为.