题目内容
10.写出(x${\;}^{6}+\frac{1}{x\sqrt{x}}$)5的展开式中常数项:5.分析 在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得展开式中常数项.
解答 解:(x${\;}^{6}+\frac{1}{x\sqrt{x}}$)5的展开式的通项公式为Tr+1=${C}_{5}^{r}$•${x}^{30-\frac{15r}{2}}$,
令30-$\frac{15r}{2}$=0,r=4,故展开式中常数项${C}_{5}^{4}$=5,
故答案为:5.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.计算${∫}_{0}^{4}$$\sqrt{16-{x}^{2}}dx$等于( )
| A. | 8π | B. | 16π | C. | 4π | D. | 32π |
2.与圆x2+y2=1和圆x2+y2-8x+7=0都相切的圆的圆心轨迹是( )
| A. | 椭圆 | |
| B. | 椭圆和双曲线的一支 | |
| C. | 双曲线和一条直线(去掉几个点) | |
| D. | 双曲线的一支和一条直线(去掉几个点) |
19.以坐标原点为对称中心,两坐标轴为对称轴的双曲线C的渐近线方程为$y=±\frac{{\sqrt{7}}}{3}x$,则双曲线C的离心率为( )
| A. | $\frac{5}{3}或\frac{4}{3}$ | B. | $\frac{{4\sqrt{7}}}{7}或\frac{4}{3}$ | C. | $\frac{{4\sqrt{7}}}{7}$ | D. | $\frac{4}{3}$ |
20.已知sin5.1°=m,则sin365.1°=( )
| A. | 1+m | B. | -m | C. | m | D. | 与m无关 |
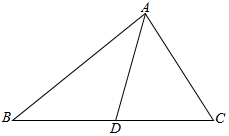 如图,在△ABC中,∠C=60°,D是BC上一点,AB=31,BD=20,AD=21.
如图,在△ABC中,∠C=60°,D是BC上一点,AB=31,BD=20,AD=21.