题目内容
春节前，有超过20万名广西，四川等省籍的外来务工人员选择驾乘摩托车沿321国道长途跋涉返乡过年，为防止摩托车驾驶人员因长途疲劳驾驶，手脚僵硬影响驾驶操作而引发交通事故，肇庆市公安交警部门在321国道沿线设立了多个长途行驶摩托车驾驶人员休息站，让过往返乡过年的摩托车驾驶人员有一个停车休息的场所．交警小李在某休息站连续5天对进站休息的驾驶人员每隔50辆摩托车就进行省籍询问一次，询问结果如图所示．
(1)问交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法；
(2)用分层抽样的方法对被询问了省籍的驾驶人员进行抽样，若广西籍的被抽取了5名，则四川籍的应抽取几名？
(3)在上述抽出的驾驶人员中任取2名，求至少有1名驾驶人员是广西籍的概率．
（1）系统抽样方法
（2）2
（3）
解析
世纪百通期末金卷系列答案 “世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时)，共有2000人参加调查,现将数据整理分组后如题中表格所示.
序号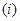 | 分组睡眠时间 | 组中值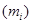 | 频数 (人数) | 频率 |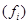
| 1 | 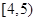 | 4.5 | 80 | ( ) |
| 2 | 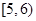 | 5.5 | 520 | 0.26 |
| 3 | 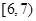 | 6.5 | 600 | 0.30 |
| 4 | 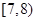 | 7.5 | ( ) | ( ) |
| 5 | 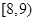 | 8.5 | 200 | 0.10 |
| 6 | 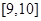 | 9.5 | 40 | 0.02 |
（1）求出表中空白处的数据，并将表格补充完整；
（2）画出频率分布直方图；
（3）为了对数据举行分析，采用了计算机辅助计算.分析中一部分计算见算法流程图，求输出的
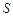值。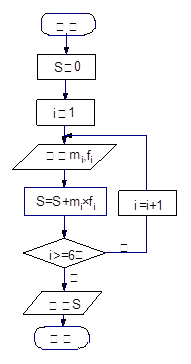
某班主任对全班50名学生的积极性和对待班级工作的态度进行了调查，
统计数据如下表所示：
| | 积极参加班级工作 | 不太积极参加班级工作 | 合计 |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
试运用独立性检验的思想方法分析：学生的学习积极性与对待班级的态度是否有关系？
|
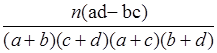
| P(K2≥k0 ) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
以下是某地搜集到的新房屋的销售价格
（万元）和房屋的面积
（
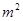）的数据 ，若由资料可知对呈线性相关关系。
| 80 | 90 | 100 | 110 | 120 |
| y | 48 | 52 | 63 | 72 | 80 |
试求:（1）线性回归方程；
（2）根据（1）的结果估计当房屋面积为
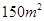时的销售价格.参考公式：
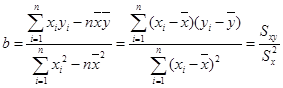
某电视台在一次对文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关数据如下表所示：
| | 文艺节目 | 新闻节目 | 总计 |
| 20岁到40岁 | 40 | 20 | 60 |
| 40岁以上 | 15 | 25 | 40 |
| 总计 | 55 | 45 | 100 |
（1）用分层抽样方法在收看新闻节目的观众中，随机抽取9名，那么40岁以上的观众应抽取几名？
（2）由表中数据分析，我们能否有99%的把握认为收看新闻节目的观众与年龄有关？（最后结果保留3位有效数字，四舍五入）
附：
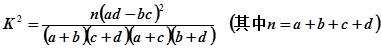
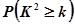 | 0.05 | 0.01 | 0.005 | 0.001 |
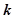 | 3.841 | 6.635 | 7.879 | 10.828 |
某人摆一个摊位卖小商品，一周内出摊天数x与盈利y(百元)，之间的一组数据关系见表：
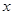 | 2 | 3 | 4 | 5 | 6 |
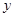 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
，
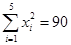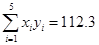，(1)在下面坐标系中画出散点图；
(2)计算
，
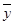，并求出线性回归方程；(3)在第(2)问条件下，估计该摊主每周7天要是天天出摊，盈利为多少?
近年来，我国很多城市都出现了严重的雾霾天气．为了更好地保护环境，2012年国家环保部发布了新修订的《环境空气质量标准》,其中规定:居民区 的PM2.5的年平均浓度不得超过35微克/立方米.某城市环保部门在2014年1月1日到 2014年3月31日这90天对某居民区的PM2. 5平均浓度的监测数据统计如下:
| 组别 | PM2.5浓度（微克/立方米） | 频数（天） |
| 第一组 | （0,35] | 24 |
| 第二组 | (35,75] | 48 |
| 第三组 | (75,115] | 12 |
| 第四组 | >115 | 6 |
（1）在这
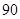天中抽取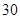
天的数据做进一步分析,每一组应抽取多少天?（2）在(I)中所抽取的样本PM2. 5的平均浓度超过75(微克/立方米)的若干天中,随 机抽取2天,求至少有一天平均浓度超过115(微克/立方米)的概率.
，
，
，
，
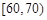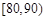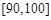的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在